Neste artigo, discutiremos a árvore de pesquisa binária. Este artigo será muito útil e informativo para os alunos com formação técnica, pois é um tópico importante do curso.
Antes de passar diretamente para a árvore de pesquisa binária, vamos primeiro ver uma breve descrição da árvore.
O que é uma árvore?
Uma árvore é um tipo de estrutura de dados usada para representar os dados em forma hierárquica. Pode ser definido como uma coleção de objetos ou entidades denominadas nós que estão interligados para simular uma hierarquia. Árvore é uma estrutura de dados não linear, pois os dados em uma árvore não são armazenados linearmente ou sequencialmente.
Agora, vamos iniciar o tópico, a árvore da Pesquisa Binária.
O que é uma árvore de pesquisa binária?
Uma árvore de pesquisa binária segue alguma ordem para organizar os elementos. Em uma árvore de pesquisa binária, o valor do nó esquerdo deve ser menor que o nó pai e o valor do nó direito deve ser maior que o nó pai. Esta regra é aplicada recursivamente às subárvores esquerda e direita da raiz.
algoritmo de agrupamento k
Vamos entender o conceito de árvore de pesquisa binária com um exemplo.
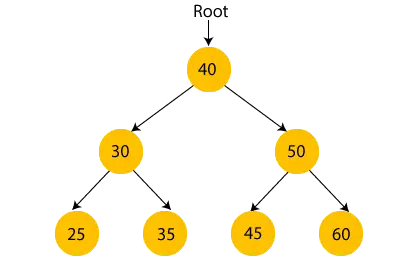
Na figura acima, podemos observar que o nó raiz é 40, e todos os nós da subárvore esquerda são menores que o nó raiz, e todos os nós da subárvore direita são maiores que o nó raiz.
Da mesma forma, podemos ver que o filho esquerdo do nó raiz é maior que o filho esquerdo e menor que o filho direito. Portanto, também satisfaz a propriedade da árvore de busca binária. Portanto, podemos dizer que a árvore da imagem acima é uma árvore binária de busca.
Suponha que se alterarmos o valor do nó 35 para 55 na árvore acima, verifique se a árvore será uma árvore de pesquisa binária ou não.

Na árvore acima, o valor do nó raiz é 40, que é maior que seu filho esquerdo 30, mas menor que seu filho direito de 30, ou seja, 55. Portanto, a árvore acima não satisfaz a propriedade da árvore de pesquisa binária. Portanto, a árvore acima não é uma árvore binária de pesquisa.
Vantagens da árvore de pesquisa binária
- Pesquisar um elemento na árvore de pesquisa binária é fácil, pois sempre temos uma dica de qual subárvore contém o elemento desejado.
- Em comparação com arrays e listas vinculadas, as operações de inserção e exclusão são mais rápidas no BST.
Exemplo de criação de uma árvore de pesquisa binária
Agora, vamos ver a criação da árvore de busca binária usando um exemplo.
Suponha que os elementos de dados sejam - 45, 15, 79, 90, 10, 55, 12, 20, 50
- Primeiro, temos que inserir Quatro cinco na árvore como a raiz da árvore.
- Então, leia o próximo elemento; se for menor que o nó raiz, insira-o como raiz da subárvore esquerda e passe para o próximo elemento.
- Caso contrário, se o elemento for maior que o nó raiz, insira-o como raiz da subárvore direita.
Agora, vamos ver o processo de criação da árvore de pesquisa binária usando o elemento de dados fornecido. O processo de criação do BST é mostrado abaixo -
Etapa 1 - Insira 45.

Etapa 2 - Insira 15.
Como 15 é menor que 45, insira-o como o nó raiz da subárvore esquerda.

Etapa 3 - Insira 79.
Como 79 é maior que 45, insira-o como o nó raiz da subárvore direita.

Etapa 4 - Insira 90.
90 é maior que 45 e 79, portanto será inserido como a subárvore direita de 79.

Etapa 5 - Insira 10.
10 é menor que 45 e 15, portanto será inserido como uma subárvore esquerda de 15.

Etapa 6 - Insira 55.
55 é maior que 45 e menor que 79, portanto será inserido como a subárvore esquerda de 79.

Etapa 7 - Insira 12.
12 é menor que 45 e 15, mas maior que 10, portanto será inserido como a subárvore direita de 10.
dobrar para string java

Etapa 8 - Insira 20.
20 é menor que 45, mas maior que 15, portanto será inserido como a subárvore direita de 15.

Etapa 9 - Insira 50.
50 é maior que 45, mas menor que 79 e 55. Portanto, será inserido como subárvore esquerda de 55.

Agora, a criação da árvore de pesquisa binária está concluída. Depois disso, vamos passar para as operações que podem ser realizadas na árvore de pesquisa binária.
Podemos realizar operações de inserção, exclusão e pesquisa na árvore de pesquisa binária.
Vamos entender como uma pesquisa é realizada em uma árvore de pesquisa binária.
Pesquisando na árvore de pesquisa binária
Pesquisar significa encontrar ou localizar um elemento ou nó específico em uma estrutura de dados. Na árvore de pesquisa binária, pesquisar um nó é fácil porque os elementos no BST são armazenados em uma ordem específica. As etapas de pesquisa de um nó na árvore de pesquisa binária são listadas a seguir -
- Primeiro, compare o elemento a ser pesquisado com o elemento raiz da árvore.
- Se root corresponder ao elemento de destino, retorne a localização do nó.
- Se não corresponder, verifique se o item é menor que o elemento raiz, se for menor que o elemento raiz e vá para a subárvore esquerda.
- Se for maior que o elemento raiz, vá para a subárvore direita.
- Repita o procedimento acima recursivamente até que a correspondência seja encontrada.
- Se o elemento não for encontrado ou não estiver presente na árvore, retorne NULL.
Agora, vamos entender a busca na árvore binária usando um exemplo. Estamos pegando a árvore de pesquisa binária formada acima. Suponha que tenhamos que encontrar o nó 20 na árvore abaixo.
Passo 1:

Passo 2:

Etapa 3:

Agora, vamos ver o algoritmo para pesquisar um elemento na árvore de pesquisa binária.
Algoritmo para pesquisar um elemento na árvore de pesquisa binária
Search (root, item) Step 1 - if (item = root → data) or (root = NULL) return root else if (item <root 2 → data) return search(root left, item) else right, end if step - < pre> <p>Now let's understand how the deletion is performed on a binary search tree. We will also see an example to delete an element from the given tree.</p> <h3>Deletion in Binary Search tree</h3> <p>In a binary search tree, we must delete a node from the tree by keeping in mind that the property of BST is not violated. To delete a node from BST, there are three possible situations occur -</p> <ul> <li>The node to be deleted is the leaf node, or,</li> <li>The node to be deleted has only one child, and,</li> <li>The node to be deleted has two children</li> </ul> <p>We will understand the situations listed above in detail.</p> <p> <strong>When the node to be deleted is the leaf node</strong> </p> <p>It is the simplest case to delete a node in BST. Here, we have to replace the leaf node with NULL and simply free the allocated space.</p> <p>We can see the process to delete a leaf node from BST in the below image. In below image, suppose we have to delete node 90, as the node to be deleted is a leaf node, so it will be replaced with NULL, and the allocated space will free.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-15.webp" alt="Binary Search tree"> <p> <strong>When the node to be deleted has only one child</strong> </p> <p>In this case, we have to replace the target node with its child, and then delete the child node. It means that after replacing the target node with its child node, the child node will now contain the value to be deleted. So, we simply have to replace the child node with NULL and free up the allocated space.</p> <p>We can see the process of deleting a node with one child from BST in the below image. In the below image, suppose we have to delete the node 79, as the node to be deleted has only one child, so it will be replaced with its child 55.</p> <p>So, the replaced node 79 will now be a leaf node that can be easily deleted.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-16.webp" alt="Binary Search tree"> <p> <strong>When the node to be deleted has two children</strong> </p> <p>This case of deleting a node in BST is a bit complex among other two cases. In such a case, the steps to be followed are listed as follows -</p> <ul> <li>First, find the inorder successor of the node to be deleted.</li> <li>After that, replace that node with the inorder successor until the target node is placed at the leaf of tree.</li> <li>And at last, replace the node with NULL and free up the allocated space.</li> </ul> <p>The inorder successor is required when the right child of the node is not empty. We can obtain the inorder successor by finding the minimum element in the right child of the node.</p> <p>We can see the process of deleting a node with two children from BST in the below image. In the below image, suppose we have to delete node 45 that is the root node, as the node to be deleted has two children, so it will be replaced with its inorder successor. Now, node 45 will be at the leaf of the tree so that it can be deleted easily.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-17.webp" alt="Binary Search tree"> <p>Now let's understand how insertion is performed on a binary search tree.</p> <h3>Insertion in Binary Search tree</h3> <p>A new key in BST is always inserted at the leaf. To insert an element in BST, we have to start searching from the root node; if the node to be inserted is less than the root node, then search for an empty location in the left subtree. Else, search for the empty location in the right subtree and insert the data. Insert in BST is similar to searching, as we always have to maintain the rule that the left subtree is smaller than the root, and right subtree is larger than the root.</p> <p>Now, let's see the process of inserting a node into BST using an example.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-18.webp" alt="Binary Search tree"> <br> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-19.webp" alt="Binary Search tree"> <h3>The complexity of the Binary Search tree</h3> <p>Let's see the time and space complexity of the Binary search tree. We will see the time complexity for insertion, deletion, and searching operations in best case, average case, and worst case.</p> <h3>1. Time Complexity</h3> <table class="table"> <tr> <th>Operations</th> <th>Best case time complexity</th> <th>Average case time complexity</th> <th>Worst case time complexity</th> </tr> <tr> <td> <strong>Insertion</strong> </td> <td>O(log n)</td> <td>O(log n)</td> <td>O(n)</td> </tr> <tr> <td> <strong>Deletion</strong> </td> <td>O(log n)</td> <td>O(log n)</td> <td>O(n)</td> </tr> <tr> <td> <strong>Search</strong> </td> <td>O(log n)</td> <td>O(log n)</td> <td>O(n)</td> </tr> </table> <p>Where 'n' is the number of nodes in the given tree.</p> <h3>2. Space Complexity</h3> <table class="table"> <tr> <th>Operations</th> <th>Space complexity</th> </tr> <tr> <td> <strong>Insertion</strong> </td> <td>O(n)</td> </tr> <tr> <td> <strong>Deletion</strong> </td> <td>O(n)</td> </tr> <tr> <td> <strong>Search</strong> </td> <td>O(n)</td> </tr> </table> <ul> <li>The space complexity of all operations of Binary search tree is O(n).</li> </ul> <h2>Implementation of Binary search tree</h2> <p>Now, let's see the program to implement the operations of Binary Search tree.</p> <p> <strong>Program:</strong> Write a program to perform operations of Binary Search tree in C++.</p> <p>In this program, we will see the implementation of the operations of binary search tree. Here, we will see the creation, inorder traversal, insertion, and deletion operations of tree.</p> <p>Here, we will see the inorder traversal of the tree to check whether the nodes of the tree are in their proper location or not. We know that the inorder traversal always gives us the data in ascending order. So, after performing the insertion and deletion operations, we perform the inorder traversal, and after traversing, if we get data in ascending order, then it is clear that the nodes are in their proper location.</p> <pre> #include using namespace std; struct Node { int data; Node *left; Node *right; }; Node* create(int item) { Node* node = new Node; node->data = item; node->left = node->right = NULL; return node; } /*Inorder traversal of the tree formed*/ void inorder(Node *root) { if (root == NULL) return; inorder(root->left); //traverse left subtree cout<data <right); traverse right subtree } node* findminimum(node* cur) *to find the inorder successor* { while(cur->left != NULL) { cur = cur->left; } return cur; } Node* insertion(Node* root, int item) /*Insert a node*/ { if (root == NULL) return create(item); /*return new node if tree is empty*/ if (item data) root->left = insertion(root->left, item); else root->right = insertion(root->right, item); return root; } void search(Node* &cur, int item, Node* &parent) { while (cur != NULL && cur->data != item) { parent = cur; if (item data) cur = cur->left; else cur = cur->right; } } void deletion(Node*& root, int item) /*function to delete a node*/ { Node* parent = NULL; Node* cur = root; search(cur, item, parent); /*find the node to be deleted*/ if (cur == NULL) return; if (cur->left == NULL && cur->right == NULL) /*When node has no children*/ { if (cur != root) { if (parent->left == cur) parent->left = NULL; else parent->right = NULL; } else root = NULL; free(cur); } else if (cur->left && cur->right) { Node* succ = findMinimum(cur->right); int val = succ->data; deletion(root, succ->data); cur->data = val; } else { Node* child = (cur->left)? cur->left: cur->right; if (cur != root) { if (cur == parent->left) parent->left = child; else parent->right = child; } else root = child; free(cur); } } int main() { Node* root = NULL; root = insertion(root, 45); root = insertion(root, 30); root = insertion(root, 50); root = insertion(root, 25); root = insertion(root, 35); root = insertion(root, 45); root = insertion(root, 60); root = insertion(root, 4); printf('The inorder traversal of the given binary tree is -
'); inorder(root); deletion(root, 25); printf('
After deleting node 25, the inorder traversal of the given binary tree is -
'); inorder(root); insertion(root, 2); printf('
After inserting node 2, the inorder traversal of the given binary tree is -
'); inorder(root); return 0; } </data></pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-20.webp" alt="Binary Search tree"> <p>So, that's all about the article. Hope the article will be helpful and informative to you.</p> <hr></root> Saída
Após a execução do código acima, a saída será -

Então, isso é tudo sobre o artigo. Espero que o artigo seja útil e informativo para você.
