- O operador Bitwise XOR também é conhecido como Exclusivo ou
- É denotado usando o '^'
- Como o nome indica, ele funciona no nível de bits dos operandos.
- O operador Bitwise XOR está na categoria de operadores Bitwise.
- No operador OR exclusivo bit a bit (XOR), dois operandos são necessários, e esses dois operandos são separados pelo símbolo XOR, ou seja, '^'.
- Para determinar a saída ou resultado obtido após a aplicação do operador XOR em dois operandos, precisamos seguir a tabela verdade lógica do operador XOR.
- XOR Truth Table é a tabela matemática construída usando a lógica adequada do operador XOR.
- A lógica usada por trás do operador XOR é; sempre que a operação XOR é aplicada nos dois diferente bits de dois operandos, então o resultado sempre produzirá '1', e se a operação XOR for aplicada nos dois mesmo bits de dois operandos, então o resultado produz a saída '0'.
Tabela verdade do operador OR exclusivo (XOR)
Sejam dois operandos; o primeiro é A e o segundo é B, o total de combinações de entrada formadas por esses dois operandos será 4. Usando a seguinte tabela verdade XOR, determinaremos a saída correspondente. O resultado será capturado em C, aqui C=A^B.
Nesta tabela verdade, estamos recebendo a entrada na forma de bits, ou seja, 0 e 1, e a saída também será gerada na forma de bits, ou seja, 0 e 1.
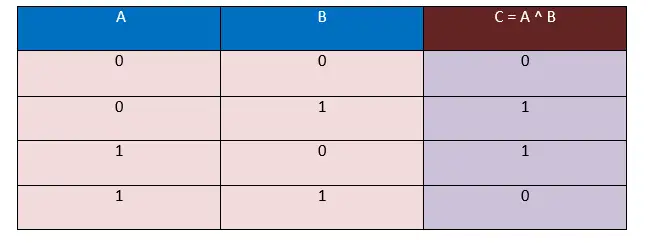
Aqui, na tabela XOR Truth acima, observamos que quando os valores dos operandos A e B são diferentes, ou seja, ( 0, 1 ), ( 1, 0 ), o resultado que sai será sempre 1. E quando o os valores dos operandos A e B são iguais, ou seja, ( 0, 0 ), ( 1, 1 ), o resultado obtido será sempre 0.
Da mesma forma, desta forma, podemos desenhar a tabela verdade para boleano valores -
Sejam dois operandos; o primeiro é A e o segundo é B . O total de combinações de entrada formadas por esses dois operandos será 4. Usando a seguinte tabela verdade XOR, determinaremos a saída correspondente. O resultado será capturado em C, aqui C = A ^ B.
Nesta tabela verdade, estamos recebendo informações na forma de valores Verdade, ou seja, Verdadeiro (T) e Falso (F). A saída também será gerada na forma de valores True, ou seja, T e F.
baixar vídeos do youtube vlc

Aqui, na tabela XOR Truth acima, observamos que, quando os valores dos operandos A e B são diferentes, ou seja, ( F, T ), ( T, F ), o resultado será sempre T. E quando o os valores dos operandos A e B são iguais, ou seja, (F, F), (T, T), o resultado será sempre F.
Pelas tabelas acima, observamos que T (Verdadeiro) é denotado por um e F (Falso) é denotado por 0.
Etapas para resolver qualquer problema -
- Os operandos dados no problema estarão sempre no valor decimal.
- Primeiramente, precisamos converter os valores dos operandos em binário
- Após converter os valores dos operandos em números binários, coloque os dois operandos um sobre o outro.
- Lembre-se que antes de aplicar a operação OR exclusiva (XOR) neles, verifique o número de dígitos neles.
- Se a contagem de dígitos não corresponder, os 0 extras na extremidade esquerda do operando pequeno equilibram as contagens de dígitos.
- Finalmente, com a ajuda da tabela verdade acima, aplique a operação XOR nos operandos um por um, pegando um bit de cada vez para aplicar a operação XOR.
- Por fim, o resultado é produzido na forma de saída.
- A saída produzida estará no formato binário, agora converta o formato binário para o formato decimal e anote o valor do resultado.
Execução da operação Bitwise Exclusive OR (XOR) em C++
Vamos entender mais detalhadamente sobre a execução da operação XOR em C++ com a ajuda de exemplos -
Exemplo 1: Encontre o OR exclusivo de valores inteiros; 10 e 14. Além disso, explique e escreva o código de execução em C++.
Solução: Vamos considerar duas variáveis, 'a' e 'b', para armazenar os dois operandos correspondentes dados na questão acima, ou seja, 10 e 14.
Aqui, a = 10 e b = 14.
Seguiremos os passos abaixo para descobrir o OR exclusivo dos dois operandos fornecidos.
- Sabemos que 10 e 14 estão na forma decimal, e para aplicar a operação XOR bit a bit é necessário convertê-la para a forma binária.
- A forma binária 'a', ou seja, 10 é '1010' e forma binária de 'b', ou seja, 14 é '1110'.
- Aqui observamos que a contagem de dígitos binários presentes em a é quatro e a contagem de dígitos binários presentes em b também é 4; portanto, o número de dígitos binários presentes em ambas as variáveis é o mesmo e já balanceado, não precisamos adicionar mais números de 0 para equilibrá-lo.
- Agora, colocando os dígitos binários presentes em 'b' nos dígitos binários presentes em 'a'.
- Por fim, aplique a operação XOR uma por uma nas correspondências de bits correspondentes e anote a saída.
- A saída gerada finalmente estará na forma binária, conforme a questão acima dada na forma decimal, portanto precisamos converter o resultado na forma decimal.
Explicação:
a = 10 (na forma decimal)
b = 14 (na forma decimal)
Agora, para um XOR b, precisamos converter aeb na forma binária -
a = 1010 (na forma binária)
b = 1110 (na forma binária)
Agora, aplicando a operação XOR em a e b -
uma = 1010
b = 1110
---------------
uma ^ b = 0100 (Em formato binário)
O resultado de a ^ b é 0100, que está na forma binária.
Agora convertendo o resultado na forma decimal, que é 4.
10 ^ 14 = 4
NOTA: Ao usar a tabela verdade XOR acima, a saída dos bits correspondentes é gerada.
Aplicaremos agora a operação XOR bit a bit em 10 e 14 na linguagem C++ e obteremos o resultado, ou seja, 4.
Código C++ para o exemplo acima:
//************************ C++ Code ****************************** #include using namespace std; int main () { int a, b, c ; // Initializing integer variables to store data values cout <' << endl ; cout <> a ; // taking a as input from user cout <> b ; // taking b as input from user c = a ^ b ; // storing XOR result of a and b in c cout << 'Applying XOR operation on a and b: '<< endl ; cout << 'a ^ b = ' << c << endl ; // Printing the output } </'> Saída

Exemplo 2: Encontre o OR exclusivo de valores inteiros; 3 e 15. Além disso, explique e escreva o código de execução em C++.
Solução: Vamos considerar duas variáveis, 'a' e 'b', para armazenar os dois operandos correspondentes dados na questão acima, ou seja, 3 e 15.
Aqui, a = 3 e b = 15.
Seguiremos os passos abaixo para descobrir o OR exclusivo dos dois operandos fornecidos.
- Sabemos que 3 e 15 estão na forma decimal, e para aplicar a operação XOR bit a bit é necessário convertê-la para a forma binária.
- A forma binária 'a', ou seja, 3 é 'onze' e forma binária de 'b', ou seja, 15 é '1111'.
- Aqui observaremos que a contagem de dígitos binários presentes em a é dois e a contagem de dígitos binários presentes em b é quatro; portanto, o número de dígitos binários presentes em ambas as variáveis não é o mesmo. Assim, desequilibrado, precisamos adicionar mais números de 0 no lado esquerdo do número binário inferior, ou seja, a, que é ' onze' , para equilibrá-lo.
- Após o balanceamento, o valor de a é '0011' , e b é '1111'.
- Agora, colocando os dígitos binários presentes em 'b' nos dígitos binários presentes em 'a'.
- Por fim, aplique a operação XOR uma por uma nas correspondências de bits correspondentes e anote a saída.
- A saída gerada finalmente estará na forma binária, conforme a questão acima dada na forma decimal, portanto precisamos converter o resultado na forma decimal.
Explicação:
a = 3 (na forma decimal)
b = 15 (na forma decimal)
Agora, para um XOR b, precisamos converter aeb na forma binária -
a = 0011 (em formato binário)
b = 1111 (na forma binária)
Agora, aplicando a operação XOR em a e b -
uma = 0011
b = 1111
---------------
uma ^ b = 1100 (Em formato binário)
O resultado de a ^ b é 1100, que está na forma binária.
Agora convertendo o resultado na forma decimal, que é 12.
char em string java
3 ^ 15 = 12
NOTA: Ao usar a tabela verdade XOR acima, a saída dos bits correspondentes é gerada.
Aplicaremos agora a operação XOR bit a bit em 3 e 15 na linguagem C++ e obteremos o resultado, ou seja, 12.
Código C++ para o exemplo acima:
//************************ C++ Code ****************************** #include using namespace std; int main () { int a, b, c ; // Initializing integer variables to store data values cout <' << endl ; cout <> a ; // taking a as input from user cout <> b ; // taking b as input from user c = a ^ b ; // storing XOR result of a and b in c cout << 'Applying XOR operation on a and b: '<< endl ; cout << 'a ^ b = ' << c << endl ; // Printing the output } </'> Saída

