A convolução é usada para muitas coisas, como calcular derivadas, detectar bordas, aplicar desfoques, etc. e tudo isso é feito usando um 'kernel de convolução'. Um kernel de convolução é uma matriz muito pequena e nesta matriz cada célula possui um número e também um ponto de ancoragem.
O ponto de ancoragem é utilizado para saber a posição do kernel em relação à imagem. Ele começa no canto superior esquerdo da imagem e se move sequencialmente em cada pixel. O kernel se sobrepõe a alguns pixels em cada posição da imagem. Cada pixel sobreposto é multiplicado e depois adicionado. E a soma é definida como o valor da posição atual.
como obter emojis de maçã no Android
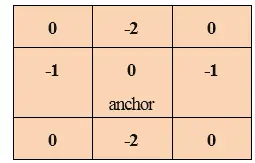
Convolução é o processo no qual cada elemento da imagem é adicionado aos seus vizinhos locais e então é ponderado pelo kernel. Está relacionado a uma forma de convolução matemática.
Na Convolução, a matriz não realiza a multiplicação tradicional de matrizes, mas é denotada por *.
Suponha que existam duas matrizes 3x3, uma é o kernel e a outra é uma peça de imagem. Na convolução, as linhas e colunas do kernel são invertidas e então multiplicadas e então a soma é realizada. Os elementos que estão presentes no centro da matriz, ou seja, em [2,2] da imagem, serão ponderados pela combinação da matriz da imagem e os pesos serão dados pelo kernel. Da mesma forma, todos os outros elementos da matriz serão ponderados e então os pesos serão calculados.
A seguir está o pseudocódigo para descrever o processo de convolução:
onde encontro as configurações do meu navegador
For each image row in input image: For each pixel in image row: Set accumulator to zero For each kernel row in kernel: For each element in kernel row: If element position corresponding* to pixel position then Multiply element value corresponding*to pixelvalue Add result to accumulator Endif Set output image pixel to accumulator
A convolução pode ser calculada usando vários loops for. Mas usar loops for causa muitos cálculos repetidos e também aumenta o tamanho da imagem e do kernel. Usando a técnica da Transformada Discreta de Fourier, o cálculo da convolução pode ser feito rapidamente. Nesta técnica, toda a operação de convolução é convertida em uma simples multiplicação.
Na convolução, o problema ocorre quando o kernel está próximo da borda ou dos cantos porque o kernel é bidimensional.
Para superar esses problemas, o seguinte pode ser feito:
- Alguns podem ser ignorados
- Pixels extras podem ser criados perto das bordas.
Pixels extras podem ser criados das seguintes maneiras:
- Pixel de borda duplicado.
- Refletir bordas
- Pixels podem ser copiados do outro lado.
