Divide and Conquer é um padrão algorítmico. Nos métodos algorítmicos, o projeto consiste em disputar uma entrada enorme, dividir a entrada em partes menores, decidir o problema em cada uma das partes pequenas e, em seguida, mesclar as soluções por partes em uma solução global. Este mecanismo de resolução do problema é denominado Estratégia Dividir e Conquistar.

O algoritmo Divide and Conquer consiste em uma disputa usando as três etapas a seguir.

Dividiro problema original em um conjunto de subproblemas.Conquistar:Resolva cada subproblema individualmente, recursivamente.Combinar:Reúna as soluções dos subproblemas para obter a solução de todo o problema.

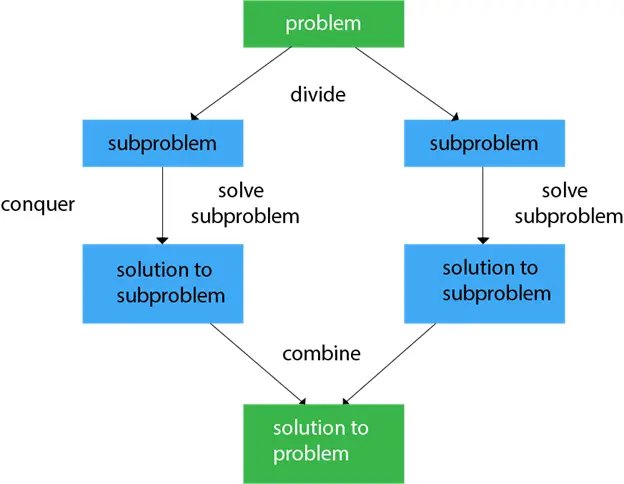
Geralmente, podemos seguir o dividir e conquistar abordagem em um processo de três etapas.

Exemplos: Os algoritmos de computador específicos são baseados na abordagem Divide & Conquer:

1. Problema Máximo e Mínimo
2. Pesquisa binária
3. Classificação (classificação por mesclagem, classificação rápida)
4. Torre de Hanói.

Fundamentos da Estratégia Dividir e Conquistar:

Existem dois fundamentos da Estratégia Divide & Conquer:

1. Fórmula Relacional
2. Condição de parada

1. Fórmula Relacional: É a fórmula que geramos a partir da técnica dada. Após a geração da Fórmula, aplicamos a Estratégia D&C, ou seja, quebramos o problema recursivamente e resolvemos os subproblemas quebrados.

2. Condição de parada: Quando resolvemos o problema usando a Estratégia Divide & Conquer, precisamos saber por quanto tempo precisamos aplicar o Divide & Conquer. Portanto, a condição em que há necessidade de interromper nossas etapas de recursão de D&C é chamada de Condição de Parada.

Aplicações da abordagem de dividir e conquistar:

Os algoritmos a seguir são baseados no conceito da Técnica de Dividir e Conquistar:

Pesquisa binária:O algoritmo de pesquisa binária é um algoritmo de pesquisa, também chamado de pesquisa de meio intervalo ou pesquisa logarítmica. Funciona comparando o valor alvo com o elemento intermediário existente em uma matriz classificada. Após fazer a comparação, se o valor for diferente, então a metade que não pode conter o alvo acabará sendo eliminada, seguindo-se a continuação da busca na outra metade. Consideraremos novamente o elemento intermediário e compará-lo-emos com o valor alvo. O processo continua se repetindo até que o valor alvo seja atingido. Se descobrirmos que a outra metade está vazia após o término da pesquisa, podemos concluir que o alvo não está presente no array.Ordenação rápida:É o algoritmo de classificação mais eficiente, também conhecido como classificação por troca de partição. Ele começa selecionando um valor pivô de uma matriz e depois dividindo o restante dos elementos da matriz em duas submatrizes. A partição é feita comparando cada um dos elementos com o valor do pivô. Ele compara se o elemento contém um valor maior ou menor que o pivô e então classifica os arrays recursivamente.Mesclar classificação:É um algoritmo de classificação que classifica um array fazendo comparações. Ele começa dividindo um array em submatrizes e, em seguida, classifica recursivamente cada um deles. Após a classificação ser concluída, ele os mescla novamente.Par de pontos mais próximo:É um problema de geometria computacional. Este algoritmo enfatiza a descoberta do par de pontos mais próximo em um espaço métrico, dados n pontos, de modo que a distância entre o par de pontos seja mínima.Algoritmo de Strassen:É um algoritmo para multiplicação de matrizes, que leva o nome de Volker Strassen. Provou ser muito mais rápido que o algoritmo tradicional quando funciona em matrizes grandes.Algoritmo Cooley-Tukey Fast Fourier Transform (FFT):O algoritmo Fast Fourier Transform recebeu o nome de J. W. Cooley e John Turkey. Segue a abordagem de dividir e conquistar e impõe uma complexidade de O(nlogn).Algoritmo Karatsuba para multiplicação rápida:É um dos algoritmos de multiplicação mais rápidos da época tradicional, inventado por Anatoly Karatsuba no final de 1960 e publicado em 1962. Ele multiplica dois números de n dígitos de forma a reduzi-los a no máximo um dígito.

Vantagens de dividir e conquistar

• Dividir para Conquistar tende a resolver com sucesso um dos maiores problemas, como a Torre de Hanói, um quebra-cabeça matemático. É um desafio resolver problemas complicados para os quais você não tem uma ideia básica, mas com a ajuda da abordagem de dividir para conquistar, o esforço diminuiu, pois trabalha para dividir o problema principal em duas metades e depois resolvê-los recursivamente. Este algoritmo é muito mais rápido que outros algoritmos.
• Ele usa a memória cache com eficiência, sem ocupar muito espaço, porque resolve subproblemas simples na memória cache, em vez de acessar a memória principal, mais lenta.
• É mais proficiente do que sua contraparte, técnica de Força Bruta.
• Como esses algoritmos inibem o paralelismo, ele não envolve nenhuma modificação e é tratado por sistemas que incorporam processamento paralelo.

Desvantagens de dividir e conquistar

• Como a maioria de seus algoritmos são projetados incorporando recursão, é necessário um alto gerenciamento de memória.
• Uma pilha explícita pode usar excessivamente o espaço.
• Pode até travar o sistema se a recursão for realizada rigorosamente maior que a pilha presente na CPU.