A programação dinâmica é uma técnica que divide os problemas em subproblemas e salva o resultado para fins futuros, para que não precisemos calcular o resultado novamente. Os subproblemas são otimizados para otimizar a solução geral, conhecida como propriedade ótima da subestrutura. O principal uso da programação dinâmica é resolver problemas de otimização. Aqui, problemas de otimização significam quando estamos tentando descobrir a solução mínima ou máxima de um problema. A programação dinâmica garante encontrar a solução ótima de um problema se a solução existir.

A definição de programação dinâmica diz que é uma técnica para resolver um problema complexo, primeiro dividindo uma coleção de subproblemas mais simples, resolvendo cada subproblema apenas uma vez e depois armazenando suas soluções para evitar cálculos repetitivos.

Vamos entender essa abordagem por meio de um exemplo.

Considere um exemplo da série Fibonacci. A série a seguir é a série de Fibonacci:

convertendo string em data

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ,…

Os números da série acima não são calculados aleatoriamente. Matematicamente, poderíamos escrever cada um dos termos usando a fórmula abaixo:

F(n) = F(n-1) + F(n-2),

Com os valores base F(0) = 0 e F(1) = 1. Para calcular os demais números, seguimos a relação acima. Por exemplo, F(2) é a soma f(0) e f(1), que é igual a 1.

Como podemos calcular F(20)?

O termo F(20) será calculado usando a enésima fórmula da série de Fibonacci. A figura abaixo mostra como F(20) é calculado.

data local

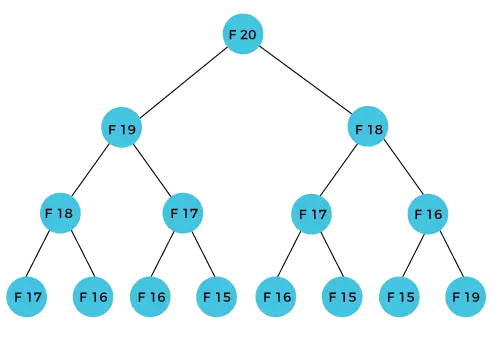
Como podemos observar na figura acima que F(20) é calculado como a soma de F(19) e F(18). Na abordagem de programação dinâmica, tentamos dividir o problema em subproblemas semelhantes. Estamos seguindo esta abordagem no caso acima, onde F(20) nos subproblemas semelhantes, ou seja, F(19) e F(18). Se recapitularmos a definição de programação dinâmica, ela diz que o subproblema semelhante não deve ser computado mais de uma vez. Ainda assim, no caso acima, o subproblema é calculado duas vezes. No exemplo acima, F(18) é calculado duas vezes; da mesma forma, F(17) também é calculado duas vezes. No entanto, esta técnica é bastante útil porque resolve subproblemas semelhantes, mas precisamos ser cautelosos ao armazenar os resultados porque não somos específicos em armazenar o resultado que calculamos uma vez, então isso pode levar ao desperdício de recursos.

No exemplo acima, se calcularmos F(18) na subárvore certa, isso levará a um tremendo uso de recursos e diminuirá o desempenho geral.

A solução para o problema acima é salvar os resultados calculados em um array. Primeiro, calculamos F(16) e F(17) e salvamos seus valores em um array. O F(18) é calculado somando os valores de F(17) e F(16), que já estão salvos em um array. O valor calculado de F(18) é salvo em uma matriz. O valor de F(19) é calculado usando a soma de F(18) e F(17), e seus valores já estão salvos em um array. O valor calculado de F(19) é armazenado em uma matriz. O valor de F(20) pode ser calculado adicionando os valores de F(19) e F(18), e os valores de F(19) e F(18) são armazenados em uma matriz. O valor final calculado de F(20) é armazenado em uma matriz.

Como funciona a abordagem de programação dinâmica?

A seguir estão as etapas que a programação dinâmica segue:

• Ele divide o problema complexo em subproblemas mais simples.
• Ele encontra a solução ótima para esses subproblemas.
• Armazena os resultados dos subproblemas (memoização). O processo de armazenamento dos resultados dos subproblemas é conhecido como memorização.
• Ele os reutiliza para que o mesmo subproblema seja calculado mais de uma vez.
• Finalmente, calcule o resultado do problema complexo.

As cinco etapas acima são as etapas básicas para programação dinâmica. A programação dinâmica é aplicável que possui propriedades como:

renomeando diretório linux

Aqueles problemas que apresentam subproblemas sobrepostos e subestruturas ótimas. Aqui, subestrutura ótima significa que a solução dos problemas de otimização pode ser obtida simplesmente combinando a solução ótima de todos os subproblemas.

No caso da programação dinâmica, a complexidade do espaço aumentaria à medida que armazenamos os resultados intermediários, mas a complexidade do tempo diminuiria.

Abordagens de programação dinâmica

Existem duas abordagens para programação dinâmica:

• Abordagem de cima para baixo
• Abordagem de baixo para cima

Abordagem de cima para baixo

A abordagem top-down segue a técnica de memorização, enquanto a abordagem bottom-up segue o método de tabulação. Aqui a memorização é igual à soma da recursão e do cache. Recursão significa chamar a própria função, enquanto cache significa armazenar os resultados intermediários.

programação c de matriz de estrutura

Vantagens

• É muito fácil de entender e implementar.
• Ele resolve os subproblemas somente quando necessário.
• É fácil depurar.

Desvantagens

Ele usa a técnica de recursão que ocupa mais memória na pilha de chamadas. Às vezes, quando a recursão é muito profunda, ocorrerá a condição de estouro de pilha.

Ocupa mais memória, o que degrada o desempenho geral.

Vamos entender a programação dinâmica através de um exemplo.

 int fib(int n) { if(n<0) error; if(n="=0)" return 0; 1; sum="fib(n-1)" + fib(n-2); } < pre> <p>In the above code, we have used the recursive approach to find out the Fibonacci series. When the value of &apos;n&apos; increases, the function calls will also increase, and computations will also increase. In this case, the time complexity increases exponentially, and it becomes 2<sup>n</sup>.</p> <p>One solution to this problem is to use the dynamic programming approach. Rather than generating the recursive tree again and again, we can reuse the previously calculated value. If we use the dynamic programming approach, then the time complexity would be O(n).</p> <p>When we apply the dynamic programming approach in the implementation of the Fibonacci series, then the code would look like:</p> <pre> static int count = 0; int fib(int n) { if(memo[n]!= NULL) return memo[n]; count++; if(n<0) error; if(n="=0)" return 0; 1; sum="fib(n-1)" + fib(n-2); memo[n]="sum;" } < pre> <p>In the above code, we have used the memorization technique in which we store the results in an array to reuse the values. This is also known as a top-down approach in which we move from the top and break the problem into sub-problems.</p> <h3>Bottom-Up approach</h3> <p>The bottom-up approach is also one of the techniques which can be used to implement the dynamic programming. It uses the tabulation technique to implement the dynamic programming approach. It solves the same kind of problems but it removes the recursion. If we remove the recursion, there is no stack overflow issue and no overhead of the recursive functions. In this tabulation technique, we solve the problems and store the results in a matrix.</p> <p>There are two ways of applying dynamic programming:</p> <ul> <tr><td>Top-Down</td>  </tr><tr><td>Bottom-Up</td>  </tr></ul> <p>The bottom-up is the approach used to avoid the recursion, thus saving the memory space. The bottom-up is an algorithm that starts from the beginning, whereas the recursive algorithm starts from the end and works backward. In the bottom-up approach, we start from the base case to find the answer for the end. As we know, the base cases in the Fibonacci series are 0 and 1. Since the bottom approach starts from the base cases, so we will start from 0 and 1.</p> <p> <strong>Key points</strong> </p> <ul> <li>We solve all the smaller sub-problems that will be needed to solve the larger sub-problems then move to the larger problems using smaller sub-problems.</li> <li>We use for loop to iterate over the sub-problems.</li> <li>The bottom-up approach is also known as the tabulation or table filling method.</li> </ul> <p> <strong>Let&apos;s understand through an example.</strong> </p> <p>Suppose we have an array that has 0 and 1 values at a[0] and a[1] positions, respectively shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-2.webp" alt="Dynamic Programming"> <p>Since the bottom-up approach starts from the lower values, so the values at a[0] and a[1] are added to find the value of a[2] shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-3.webp" alt="Dynamic Programming"> <p>The value of a[3] will be calculated by adding a[1] and a[2], and it becomes 2 shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-4.webp" alt="Dynamic Programming"> <p>The value of a[4] will be calculated by adding a[2] and a[3], and it becomes 3 shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-5.webp" alt="Dynamic Programming"> <p>The value of a[5] will be calculated by adding the values of a[4] and a[3], and it becomes 5 shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-6.webp" alt="Dynamic Programming"> <p>The code for implementing the Fibonacci series using the bottom-up approach is given below:</p> <pre> int fib(int n) { int A[]; A[0] = 0, A[1] = 1; for( i=2; i<=n; i++) { a[i]="A[i-1]" + a[i-2] } return a[n]; < pre> <p>In the above code, base cases are 0 and 1 and then we have used for loop to find other values of Fibonacci series.</p> <p> <strong>Let&apos;s understand through the diagrammatic representation.</strong> </p> <p>Initially, the first two values, i.e., 0 and 1 can be represented as:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-7.webp" alt="Dynamic Programming"> <p>When i=2 then the values 0 and 1 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-8.webp" alt="Dynamic Programming"> <p>When i=3 then the values 1and 1 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-9.webp" alt="Dynamic Programming"> <p>When i=4 then the values 2 and 1 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-10.webp" alt="Dynamic Programming"> <p>When i=5, then the values 3 and 2 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-11.webp" alt="Dynamic Programming"> <p>In the above case, we are starting from the bottom and reaching to the top.</p> <hr></=n;></pre></0)></pre></0)>