A árvore de expressão é uma árvore usada para representar as várias expressões. A estrutura de dados em árvore é usada para representar as instruções expressionais. Nesta árvore, o nó interno sempre denota os operadores.
- Os nós folha sempre denotam os operandos.
- As operações são sempre realizadas nesses operandos.
- O operador presente na profundidade da árvore tem sempre a prioridade mais alta.
- O operador que não está muito na profundidade da árvore está sempre na prioridade mais baixa em comparação com os operadores que estão na profundidade.
- O operando sempre estará presente na profundidade da árvore; por isso é considerado o Prioridade máxima entre todos os operadores.
- Resumindo, podemos resumir como o valor presente na profundidade da árvore tem a prioridade mais alta em comparação com os outros operadores presentes no topo da árvore.
- O principal uso dessas árvores de expressão é que elas são usadas para avaliar, analisar e modificar as diversas expressões.
- Também é usado para descobrir a associatividade de cada operador na expressão.
- Por exemplo, o operador + é associativo à esquerda e / é associativo à direita.
- O dilema desta associatividade foi resolvido usando a expressão árvores.
- Essas árvores de expressão são formadas usando uma gramática livre de contexto.
- Associamos uma regra em gramáticas livres de contexto na frente de cada produção gramatical.
- Essas regras também são conhecidas como regras semânticas e, usando essas regras semânticas, podemos construir facilmente as árvores de expressão.
- É uma das partes principais do projeto do compilador e pertence à fase de análise semântica.
- Nesta análise semântica, utilizaremos as traduções direcionadas à sintaxe e, na forma de saída, produziremos a árvore de análise anotada.
- Uma árvore de análise anotada nada mais é do que a análise simples associada ao atributo type e a cada regra de produção.
- O principal objetivo do uso das árvores de expressão é fazer expressões complexas e que possam ser facilmente avaliadas usando essas árvores de expressão.
- É imutável e, uma vez criada uma árvore de expressão, não podemos alterá-la ou modificá-la ainda mais.
- Para fazer mais modificações, é necessário construir totalmente a nova árvore de expressão.
- Também é usado para resolver a avaliação de expressões postfixas, prefixas e infixas.
As árvores de expressão desempenham um papel muito importante na representação do nível de idioma código na forma de dados, que são armazenados principalmente na estrutura em forma de árvore. Também é usado na representação de memória do lambda expressão. Usando a estrutura de dados em árvore, podemos expressar a expressão lambda de forma mais transparente e explícita. Ele é criado primeiro para converter o segmento de código em segmento de dados para que a expressão possa ser facilmente avaliada.
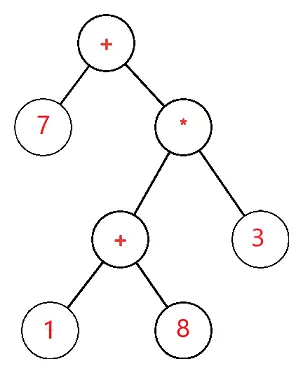
A árvore de expressão é uma árvore binária em que cada nó externo ou folha corresponde ao operando e cada nó interno ou pai corresponde aos operadores, então, por exemplo, árvore de expressão para 7 + ((1+8)*3) seria:
Seja S a árvore de expressão
Se S não for nulo, então
Se S.value for um operando, então
Retornar S.valor
x = resolver (S.esquerda)
y = resolver (S.direito)
Retornar calcular (x, y, S.valor)
Aqui no exemplo acima, a árvore de expressões usou gramática livre de contexto.
Temos algumas produções associadas a algumas regras de produção nesta gramática, conhecidas principalmente como regras semânticas . Podemos definir a produção de resultados a partir das regras de produção correspondentes usando essas regras semânticas. Aqui usamos o parâmetro value, que calculará o resultado e o retornará ao símbolo inicial da gramática. S.left calculará o filho esquerdo do nó e, da mesma forma, o filho direito do nó pode ser calculado usando o parâmetro S.right.
Uso da árvore de expressão
- O principal objetivo do uso das árvores de expressão é fazer expressões complexas e que possam ser facilmente avaliadas usando essas árvores de expressão.
- Também é usado para descobrir a associatividade de cada operador na expressão.
- Também é usado para resolver a avaliação de expressões postfixas, prefixas e infixas.
Implementação de uma árvore de expressão
Para implementar a árvore de expressão e escrever seu programa, seremos obrigados a usar uma estrutura de dados de pilha.
Como sabemos que a pilha é baseada no princípio LIFO do último a entrar, primeiro a sair, o elemento de dados inserido recentemente na pilha foi retirado sempre que necessário. Para sua implementação são utilizadas as duas principais operações da pilha, push e pop. Usando a operação push, colocaremos o elemento de dados na pilha e, usando a operação pop, removeremos o elemento de dados da pilha.
Principais funções da pilha na implementação da árvore de expressão:
Em primeiro lugar, faremos a varredura da expressão dada da esquerda para a direita e, em seguida, verificaremos um por um o caractere identificado,
- Se um caractere digitalizado for um operando, aplicaremos a operação push e o colocaremos na pilha.
- Se um personagem digitalizado for um operador, aplicaremos a operação pop nele para remover os dois valores da pilha para torná-los seus filhos e, depois disso, colocaremos de volta o nó pai atual na pilha.
Implementação de árvore de expressão em linguagem de programação C
// C program for expression tree implementation #include #include /* The below structure node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ struct node { char info ; struct node* l ; struct node* r ; struct node* nxt ; }; struct node *head=NULL; /* Helper function that allocates a new node with the given data and NULL left and right pointers. */ struct node* newnode(char data) { struct node* node = (struct node*) malloc ( sizeof ( struct node ) ) ; node->info = data ; node->l = NULL ; node->r = NULL ; node->nxt = NULL ; return ( node ) ; } void Inorder(struct node* node) { if ( node == NULL) return ; else { /* first recur on left child */ Inorder ( node->l ) ; /* then print the data of node */ printf ( '%c ' , node->info ) ; /* now recur on right child */ Inorder ( node->r ) ; } } void push ( struct node* x ) { if ( head == NULL ) head = x ; else { ( x )->nxt = head ; head = x ; } // struct node* temp ; // while ( temp != NULL ) // { // printf ( ' %c ' , temp->info ) ; // temp = temp->nxt ; // } } struct node* pop() { // Poping out the top most [pointed with head] element struct node* n = head ; head = head->nxt ; return n ; } int main() { char t[] = { 'X' , 'Y' , 'Z' , '*' , '+' , 'W' , '/' } ; int n = sizeof(t) / sizeof(t[0]) ; int i ; struct node *p , *q , *s ; for ( i = 0 ; i <n ; i++ ) { if read character is operator then popping two other elements from stack and making a binary tree ( t[i]="=" '+' || '-' '*' ' '^' s="newnode" t [ i ] p="pop()" q="pop()" s->l = q ; s->r = p; push(s); } else { s = newnode ( t [ i ] ) ; push ( s ) ; } } printf ( ' The Inorder Traversal of Expression Tree: ' ) ; Inorder ( s ) ; return 0 ; } </n> A saída do programa acima é:
X + Y * Z / W
Implementação de árvore de expressões em linguagem de programação C++
// C++ program for expression tree #include using namespace std ; /* The below class node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ class node { public: char info ; node* l ; node* r ; node* nxt = NULL ; node ( char c ) { this->info = c ; l = NULL ; r = NULL ; } node() { l = NULL ; r = NULL ; } friend class Stack ; friend class tree ; } ; class Stack { node* head = NULL ; public: void push ( node* ) ; node* pop() ; friend class tree ; } ; class tree { public: void inorder ( node* x ) { // cout<<'tree in inorder traversal is: '<l ) ; cout <info <r } void stack::push( node* x { if ( head="=" null we are inserting here nodes at the top of stack [following lifo principle] else x->nxt = head ; head = x ; } } node* Stack::pop() { // Poping out the top most [ pointed with head ] element node* p = head ; head = head->nxt ; return p ; } int main() { string str = 'XYZ*+W/' ; // If you wish take input from user: //cout << 'Insert Postorder Expression: ' <> s; Stack s ; tree t ; node *p, *q, *re; int n = str.length() ; for ( int i = 0 ; i <n ; i++ ) { if ( str[ i ]="=" '+' || '-' '*' ' '^') re="new" node( str[i] p="s.pop()" q="s.pop()" re->l = q ; re->r = p ; s.push(re) ; } else { re = new node( str[ i ] ) ; s.push(re) ; } } cout << ' The Inorder Traversal of Expression Tree: ' ; t.inorder(re) ; return 0 ; } </n></'tree> A saída do programa acima é:
X + Y * Z / W
Implementação da árvore de expressões na linguagem de programação Java
// Java program for expression tree import java.util.* ; /* The below class node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ class Node { char info ; Node l , r ; public Node(char data) { this.info = data ; l = null ; r = null ; } } public class Main { public static boolean isOperator ( char ch ) { if ( ch == '+' || ch == '-' || ch == '*' || ch == '/' || ch == '^' ) { return true ; } return false ; } public static Node Tree ( String postfix ) { Stack st = new Stack(); Node t1,t2,temp ; for ( int i = 0 ; i <p> <strong>The output of the above program is:</strong> </p> <pre> X + Y * Z / W </pre> <hr> 