 #practiceLinkDiv { display: nenhum! Importante; }
#practiceLinkDiv { display: nenhum! Importante; }O algoritmo de exclusão reversa está intimamente relacionado a Algoritmo de Kruskal . No algoritmo de Kruskal, o que fazemos é: Classificar as arestas em ordem crescente de seus pesos. Depois de classificar, escolhemos as arestas uma por uma em ordem crescente. Incluímos a aresta escolhida atual se, ao incluí-la na árvore geradora, não formarmos nenhum ciclo até que haja arestas V-1 na árvore geradora, onde V = número de vértices.
No algoritmo Reverse Delete, classificamos todas as arestas em diminuindo ordem de seus pesos. Depois de classificar, escolhemos as arestas uma por uma em ordem decrescente. Nós inclua a borda atual escolhida se a exclusão da borda atual causar desconexão no gráfico atual . A ideia principal é excluir aresta se sua exclusão não levar à desconexão do grafo.
escreva json no arquivo python
O Algoritmo:
- Classifique todas as arestas do gráfico em ordem não crescente de pesos das arestas.
- Inicialize o MST como gráfico original e remova arestas extras usando a etapa 3.
- Escolha a aresta de maior peso das arestas restantes e verifique se a exclusão da aresta desconecta o gráfico ou não .
Se desconectar, não excluímos a borda.
Caso contrário, excluímos a borda e continuamos.
Ilustração:
Vamos entender com o seguinte exemplo:
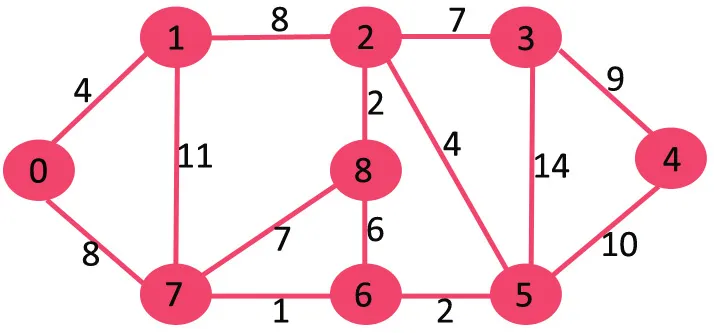
Se excluirmos a borda de maior peso do gráfico de peso 14, ela não será desconectada, então a removemos.
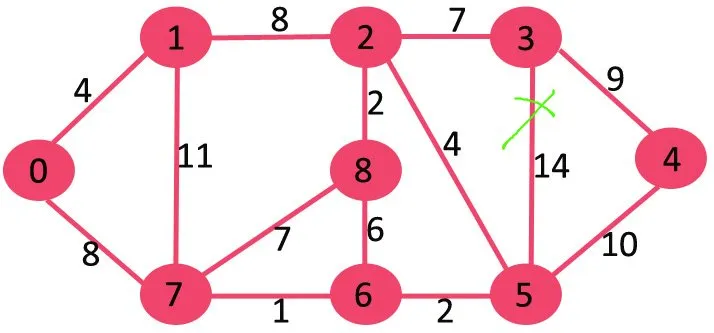
Em seguida, excluímos 11, pois excluí-lo não desconecta o gráfico.
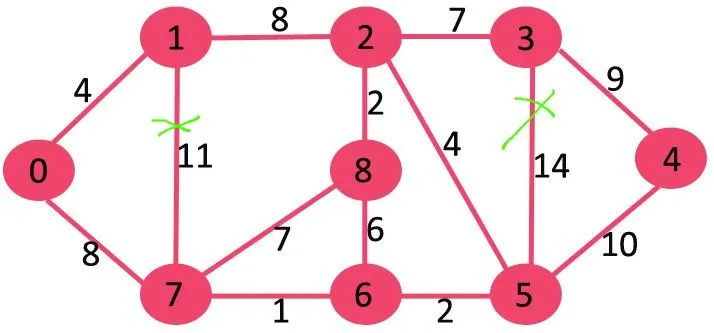
Em seguida, excluímos 10, pois excluí-lo não desconecta o gráfico.

O próximo é 9. Não podemos excluir 9, pois excluí-lo causa desconexão.
como mudar string para int

Continuamos assim e as arestas seguintes permanecem no MST final.
Edges in MST
(3 4)
(0 7)
(2 3)
(2 5)
(0 1)
(5 6)
(2 8)
(6 7)
Observação : No caso de arestas com o mesmo peso, podemos escolher qualquer aresta com arestas com o mesmo peso.
Prática recomendada Algoritmo de exclusão reversa para árvore de abrangência mínima Experimente!Implementação:
C++// C++ program to find Minimum Spanning Tree // of a graph using Reverse Delete Algorithm #include
// Java program to find Minimum Spanning Tree // of a graph using Reverse Delete Algorithm import java.util.*; // class to represent an edge class Edge implements Comparable<Edge> { int u v w; Edge(int u int v int w) { this.u = u; this.w = w; this.v = v; } public int compareTo(Edge other) { return (this.w - other.w); } } // Class to represent a graph using adjacency list // representation public class GFG { private int V; // No. of vertices private List<Integer>[] adj; private List<Edge> edges; @SuppressWarnings({ 'unchecked' 'deprecated' }) public GFG(int v) // Constructor { V = v; adj = new ArrayList[v]; for (int i = 0; i < v; i++) adj[i] = new ArrayList<Integer>(); edges = new ArrayList<Edge>(); } // function to Add an edge public void AddEdge(int u int v int w) { adj[u].add(v); // Add w to v’s list. adj[v].add(u); // Add w to v’s list. edges.add(new Edge(u v w)); } // function to perform dfs private void DFS(int v boolean[] visited) { // Mark the current node as visited and print it visited[v] = true; // Recur for all the vertices adjacent to // this vertex for (int i : adj[v]) { if (!visited[i]) DFS(i visited); } } // Returns true if given graph is connected else false private boolean IsConnected() { boolean[] visited = new boolean[V]; // Find all reachable vertices from first vertex DFS(0 visited); // If set of reachable vertices includes all // return true. for (int i = 1; i < V; i++) { if (visited[i] == false) return false; } return true; } // This function assumes that edge (u v) // exists in graph or not public void ReverseDeleteMST() { // Sort edges in increasing order on basis of cost Collections.sort(edges); int mst_wt = 0; // Initialize weight of MST System.out.println('Edges in MST'); // Iterate through all sorted edges in // decreasing order of weights for (int i = edges.size() - 1; i >= 0; i--) { int u = edges.get(i).u; int v = edges.get(i).v; // Remove edge from undirected graph adj[u].remove(adj[u].indexOf(v)); adj[v].remove(adj[v].indexOf(u)); // Adding the edge back if removing it // causes disconnection. In this case this // edge becomes part of MST. if (IsConnected() == false) { adj[u].add(v); adj[v].add(u); // This edge is part of MST System.out.println('(' + u + ' ' + v + ')'); mst_wt += edges.get(i).w; } } System.out.println('Total weight of MST is ' + mst_wt); } // Driver code public static void main(String[] args) { // create the graph given in above figure int V = 9; GFG g = new GFG(V); // making above shown graph g.AddEdge(0 1 4); g.AddEdge(0 7 8); g.AddEdge(1 2 8); g.AddEdge(1 7 11); g.AddEdge(2 3 7); g.AddEdge(2 8 2); g.AddEdge(2 5 4); g.AddEdge(3 4 9); g.AddEdge(3 5 14); g.AddEdge(4 5 10); g.AddEdge(5 6 2); g.AddEdge(6 7 1); g.AddEdge(6 8 6); g.AddEdge(7 8 7); g.ReverseDeleteMST(); } } // This code is contributed by Prithi_Dey
# Python3 program to find Minimum Spanning Tree # of a graph using Reverse Delete Algorithm # Graph class represents a directed graph # using adjacency list representation class Graph: def __init__(self v): # No. of vertices self.v = v self.adj = [0] * v self.edges = [] for i in range(v): self.adj[i] = [] # function to add an edge to graph def addEdge(self u: int v: int w: int): self.adj[u].append(v) # Add w to v’s list. self.adj[v].append(u) # Add w to v’s list. self.edges.append((w (u v))) def dfs(self v: int visited: list): # Mark the current node as visited and print it visited[v] = True # Recur for all the vertices adjacent to # this vertex for i in self.adj[v]: if not visited[i]: self.dfs(i visited) # Returns true if graph is connected # Returns true if given graph is connected else false def connected(self): visited = [False] * self.v # Find all reachable vertices from first vertex self.dfs(0 visited) # If set of reachable vertices includes all # return true. for i in range(1 self.v): if not visited[i]: return False return True # This function assumes that edge (u v) # exists in graph or not def reverseDeleteMST(self): # Sort edges in increasing order on basis of cost self.edges.sort(key = lambda a: a[0]) mst_wt = 0 # Initialize weight of MST print('Edges in MST') # Iterate through all sorted edges in # decreasing order of weights for i in range(len(self.edges) - 1 -1 -1): u = self.edges[i][1][0] v = self.edges[i][1][1] # Remove edge from undirected graph self.adj[u].remove(v) self.adj[v].remove(u) # Adding the edge back if removing it # causes disconnection. In this case this # edge becomes part of MST. if self.connected() == False: self.adj[u].append(v) self.adj[v].append(u) # This edge is part of MST print('( %d %d )' % (u v)) mst_wt += self.edges[i][0] print('Total weight of MST is' mst_wt) # Driver Code if __name__ == '__main__': # create the graph given in above figure V = 9 g = Graph(V) # making above shown graph g.addEdge(0 1 4) g.addEdge(0 7 8) g.addEdge(1 2 8) g.addEdge(1 7 11) g.addEdge(2 3 7) g.addEdge(2 8 2) g.addEdge(2 5 4) g.addEdge(3 4 9) g.addEdge(3 5 14) g.addEdge(4 5 10) g.addEdge(5 6 2) g.addEdge(6 7 1) g.addEdge(6 8 6) g.addEdge(7 8 7) g.reverseDeleteMST() # This code is contributed by # sanjeev2552
// C# program to find Minimum Spanning Tree // of a graph using Reverse Delete Algorithm using System; using System.Collections.Generic; // class to represent an edge public class Edge : IComparable<Edge> { public int u v w; public Edge(int u int v int w) { this.u = u; this.v = v; this.w = w; } public int CompareTo(Edge other) { return this.w.CompareTo(other.w); } } // Graph class represents a directed graph // using adjacency list representation public class Graph { private int V; // No. of vertices private List<int>[] adj; private List<Edge> edges; public Graph(int v) // Constructor { V = v; adj = new List<int>[ v ]; for (int i = 0; i < v; i++) adj[i] = new List<int>(); edges = new List<Edge>(); } // function to Add an edge public void AddEdge(int u int v int w) { adj[u].Add(v); // Add w to v’s list. adj[v].Add(u); // Add w to v’s list. edges.Add(new Edge(u v w)); } // function to perform dfs private void DFS(int v bool[] visited) { // Mark the current node as visited and print it visited[v] = true; // Recur for all the vertices adjacent to // this vertex foreach(int i in adj[v]) { if (!visited[i]) DFS(i visited); } } // Returns true if given graph is connected else false private bool IsConnected() { bool[] visited = new bool[V]; // Find all reachable vertices from first vertex DFS(0 visited); // If set of reachable vertices includes all // return true. for (int i = 1; i < V; i++) { if (visited[i] == false) return false; } return true; } // This function assumes that edge (u v) // exists in graph or not public void ReverseDeleteMST() { // Sort edges in increasing order on basis of cost edges.Sort(); int mst_wt = 0; // Initialize weight of MST Console.WriteLine('Edges in MST'); // Iterate through all sorted edges in // decreasing order of weights for (int i = edges.Count - 1; i >= 0; i--) { int u = edges[i].u; int v = edges[i].v; // Remove edge from undirected graph adj[u].Remove(v); adj[v].Remove(u); // Adding the edge back if removing it // causes disconnection. In this case this // edge becomes part of MST. if (IsConnected() == false) { adj[u].Add(v); adj[v].Add(u); // This edge is part of MST Console.WriteLine('({0} {1})' u v); mst_wt += edges[i].w; } } Console.WriteLine('Total weight of MST is {0}' mst_wt); } } class GFG { // Driver code static void Main(string[] args) { // create the graph given in above figure int V = 9; Graph g = new Graph(V); // making above shown graph g.AddEdge(0 1 4); g.AddEdge(0 7 8); g.AddEdge(1 2 8); g.AddEdge(1 7 11); g.AddEdge(2 3 7); g.AddEdge(2 8 2); g.AddEdge(2 5 4); g.AddEdge(3 4 9); g.AddEdge(3 5 14); g.AddEdge(4 5 10); g.AddEdge(5 6 2); g.AddEdge(6 7 1); g.AddEdge(6 8 6); g.AddEdge(7 8 7); g.ReverseDeleteMST(); } } // This code is contributed by cavi4762
// Javascript program to find Minimum Spanning Tree // of a graph using Reverse Delete Algorithm // Graph class represents a directed graph // using adjacency list representation class Graph { // Constructor constructor(V) { this.V = V; this.adj = []; this.edges = []; for (let i = 0; i < V; i++) { this.adj[i] = []; } } // function to add an edge to graph addEdge(u v w) { this.adj[u].push(v);// Add w to v’s list. this.adj[v].push(u);// Add w to v’s list. this.edges.push([w [u v]]); } DFS(v visited) { // Mark the current node as visited and print it visited[v] = true; for (const i of this.adj[v]) { if (!visited[i]) { this.DFS(i visited); } } } // Returns true if given graph is connected else false isConnected() { const visited = []; for (let i = 0; i < this.V; i++) { visited[i] = false; } // Find all reachable vertices from first vertex this.DFS(0 visited); // If set of reachable vertices includes all // return true. for (let i = 1; i < this.V; i++) { if (!visited[i]) { return false; } } return true; } // This function assumes that edge (u v) // exists in graph or not reverseDeleteMST() { // Sort edges in increasing order on basis of cost this.edges.sort((a b) => a[0] - b[0]); let mstWt = 0;// Initialize weight of MST console.log('Edges in MST'); // Iterate through all sorted edges in // decreasing order of weights for (let i = this.edges.length - 1; i >= 0; i--) { const [u v] = this.edges[i][1]; // Remove edge from undirected graph this.adj[u] = this.adj[u].filter(x => x !== v); this.adj[v] = this.adj[v].filter(x => x !== u); // Adding the edge back if removing it // causes disconnection. In this case this // edge becomes part of MST. if (!this.isConnected()) { this.adj[u].push(v); this.adj[v].push(u); // This edge is part of MST console.log(`(${u} ${v})`); mstWt += this.edges[i][0]; } } console.log(`Total weight of MST is ${mstWt}`); } } // Driver code function main() { // create the graph given in above figure var V = 9; var g = new Graph(V); // making above shown graph g.addEdge(0 1 4); g.addEdge(0 7 8); g.addEdge(1 2 8); g.addEdge(1 7 11); g.addEdge(2 3 7); g.addEdge(2 8 2); g.addEdge(2 5 4); g.addEdge(3 4 9); g.addEdge(3 5 14); g.addEdge(4 5 10); g.addEdge(5 6 2); g.addEdge(6 7 1); g.addEdge(6 8 6); g.addEdge(7 8 7); g.reverseDeleteMST(); } main();
Saída
Edges in MST (3 4) (0 7) (2 3) (2 5) (0 1) (5 6) (2 8) (6 7) Total weight of MST is 37
Complexidade de tempo: O((E*(V+E)) + E log E) onde E é o número de arestas.
Complexidade do espaço: O(V+E) onde V é o número de vértices e E é o número de arestas. Estamos usando uma lista de adjacências para armazenar o gráfico, então precisamos de espaço proporcional a O(V+E).
Notas:
- A implementação acima é uma implementação simples/ingênua do algoritmo Reverse Delete e pode ser otimizada para O(E log V (log log V)3) [Fonte : Uma semana ]. Mas esta complexidade de tempo otimizada ainda é menor do que Primo e Kruskal Algoritmos para MST.
- A implementação acima modifica o gráfico original. Podemos criar uma cópia do gráfico se o gráfico original precisar ser mantido.
Criar questionário
