O algoritmo Bellman Ford é um algoritmo de caminho mais curto de fonte única. Este algoritmo é usado para encontrar a distância mais curta de um único vértice a todos os outros vértices de um gráfico ponderado. Existem vários outros algoritmos usados para encontrar o caminho mais curto, como o algoritmo de Dijkstra, etc. Se o gráfico ponderado contém valores de peso negativos, então o algoritmo de Dijkstra não confirma se produz a resposta correta ou não. Em contraste com o algoritmo Dijkstra, o algoritmo Bellman Ford garante a resposta correta mesmo se o gráfico ponderado contiver os valores de peso negativos.
Regra deste algoritmo
We will go on relaxing all the edges (n - 1) times where, n = number of vertices
Considere o gráfico abaixo:
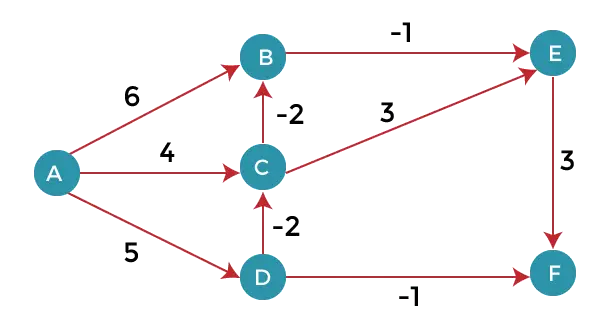
Como podemos observar no gráfico acima que alguns dos pesos são negativos. O gráfico acima contém 6 vértices, então continuaremos relaxando até os 5 vértices. Aqui, vamos relaxar todas as arestas 5 vezes. O loop irá iterar 5 vezes para obter a resposta correta. Se o loop for iterado mais de 5 vezes, a resposta também será a mesma, ou seja, não haverá alteração na distância entre os vértices.
Relaxar significa:
javafx no Eclipse
If (d(u) + c(u , v) <d(v)) d(v)="d(u)" + c(u , v) < pre> <p>To find the shortest path of the above graph, the first step is note down all the edges which are given below:</p> <p>(A, B), (A, C), (A, D), (B, E), (C, E), (D, C), (D, F), (E, F), (C, B)</p> <p>Let's consider the source vertex as 'A'; therefore, the distance value at vertex A is 0 and the distance value at all the other vertices as infinity shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-2.webp" alt="Bellman-Ford Algorithm"> <p>Since the graph has six vertices so it will have five iterations.</p> <p> <strong>First iteration</strong> </p> <p>Consider the edge (A, B). Denote vertex 'A' as 'u' and vertex 'B' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 6</p> <p>Since (0 + 6) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 6 = 6</p> <p>Therefore, the distance of vertex B is 6.</p> <p>Consider the edge (A, C). Denote vertex 'A' as 'u' and vertex 'C' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 4</p> <p>Since (0 + 4) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 4 = 4</p> <p>Therefore, the distance of vertex C is 4.</p> <p>Consider the edge (A, D). Denote vertex 'A' as 'u' and vertex 'D' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 5</p> <p>Since (0 + 5) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 5 = 5</p> <p>Therefore, the distance of vertex D is 5.</p> <p>Consider the edge (B, E). Denote vertex 'B' as 'u' and vertex 'E' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 6</p> <p>d(v) = ∞</p> <p>c(u , v) = -1</p> <p>Since (6 - 1) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 6 - 1= 5</p> <p>Therefore, the distance of vertex E is 5.</p> <p>Consider the edge (C, E). Denote vertex 'C' as 'u' and vertex 'E' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 4</p> <p>d(v) = 5</p> <p>c(u , v) = 3</p> <p>Since (4 + 3) is greater than 5, so there will be no updation. The value at vertex E is 5.</p> <p>Consider the edge (D, C). Denote vertex 'D' as 'u' and vertex 'C' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 5</p> <p>d(v) = 4</p> <p>c(u , v) = -2</p> <p>Since (5 -2) is less than 4, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 5 - 2 = 3</p> <p>Therefore, the distance of vertex C is 3.</p> <p>Consider the edge (D, F). Denote vertex 'D' as 'u' and vertex 'F' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 5</p> <p>d(v) = ∞</p> <p>c(u , v) = -1</p> <p>Since (5 -1) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 5 - 1 = 4</p> <p>Therefore, the distance of vertex F is 4.</p> <p>Consider the edge (E, F). Denote vertex 'E' as 'u' and vertex 'F' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 5</p> <p>d(v) = ∞</p> <p>c(u , v) = 3</p> <p>Since (5 + 3) is greater than 4, so there would be no updation on the distance value of vertex F.</p> <p>Consider the edge (C, B). Denote vertex 'C' as 'u' and vertex 'B' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 3</p> <p>d(v) = 6</p> <p>c(u , v) = -2</p> <p>Since (3 - 2) is less than 6, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 3 - 2 = 1</p> <p>Therefore, the distance of vertex B is 1.</p> <p>Now the first iteration is completed. We move to the second iteration.</p> <p> <strong>Second iteration:</strong> </p> <p>In the second iteration, we again check all the edges. The first edge is (A, B). Since (0 + 6) is greater than 1 so there would be no updation in the vertex B.</p> <p>The next edge is (A, C). Since (0 + 4) is greater than 3 so there would be no updation in the vertex C.</p> <p>The next edge is (A, D). Since (0 + 5) equals to 5 so there would be no updation in the vertex D.</p> <p>The next edge is (B, E). Since (1 - 1) equals to 0 which is less than 5 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(E) = d(B) +c(B , E)</p> <p>= 1 - 1 = 0</p> <p>The next edge is (C, E). Since (3 + 3) equals to 6 which is greater than 5 so there would be no updation in the vertex E.</p> <p>The next edge is (D, C). Since (5 - 2) equals to 3 so there would be no updation in the vertex C.</p> <p>The next edge is (D, F). Since (5 - 1) equals to 4 so there would be no updation in the vertex F.</p> <p>The next edge is (E, F). Since (5 + 3) equals to 8 which is greater than 4 so there would be no updation in the vertex F.</p> <p>The next edge is (C, B). Since (3 - 2) equals to 1` so there would be no updation in the vertex B.</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-3.webp" alt="Bellman-Ford Algorithm"> <p> <strong>Third iteration</strong> </p> <p>We will perform the same steps as we did in the previous iterations. We will observe that there will be no updation in the distance of vertices.</p> <pre> The following are the distances of vertices: A: 0 B: 1 C: 3 D: 5 E: 0 F: 3 </pre> <p> <strong>Time Complexity</strong> </p> <p>The time complexity of Bellman ford algorithm would be O(E|V| - 1).</p> <pre> function bellmanFord(G, S) for each vertex V in G distance[V] <- 0 infinite previous[v] <- null distance[s] for each vertex v in g edge (u,v) tempdistance distance[u] + edge_weight(u, v) if < distance[v] u distance[v} error: negative cycle exists return distance[], previous[] pre> <p> <strong>Drawbacks of Bellman ford algorithm</strong> </p> <ul> <li>The bellman ford algorithm does not produce a correct answer if the sum of the edges of a cycle is negative. Let's understand this property through an example. Consider the below graph. <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-4.webp" alt="Bellman-Ford Algorithm"></li> <li>In the above graph, we consider vertex 1 as the source vertex and provides 0 value to it. We provide infinity value to other vertices shown as below: <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-5.webp" alt="Bellman-Ford Algorithm"> <br>Edges can be written as: <br> (1, 3), (1, 2), (2, 4), (3, 2), (4, 3) </li> </ul> <p> <strong>First iteration</strong> </p> <p> <strong>Consider the edge (1, 3). Denote vertex '1' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 5</p> <p>Since (0 + 5) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 5 = 5</p> <p>Therefore, the distance of vertex 3 is 5.</p> <p> <strong>Consider the edge (1, 2). Denote vertex '1' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 4</p> <p>Since (0 + 4) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 4 = 4</p> <p>Therefore, the distance of vertex 2 is 4.</p> <p> <strong>Consider the edge (3, 2). Denote vertex '3' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 5</p> <p>d(v) = 4</p> <p>c(u , v) = 7</p> <p>Since (5 + 7) is greater than 4, so there would be no updation in the vertex 2.</p> <p> <strong>Consider the edge (2, 4). Denote vertex '2' as 'u' and vertex '4' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 4</p> <p>d(v) = ∞</p> <p>c(u , v) = 7</p> <p>Since (4 + 7) equals to 11 which is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 4 + 7 = 11</p> <p>Therefore, the distance of vertex 4 is 11.</p> <p> <strong>Consider the edge (4, 3). Denote vertex '4' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 11</p> <p>d(v) = 5</p> <p>c(u , v) = -15</p> <p>Since (11 - 15) equals to -4 which is less than 5, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 11 - 15 = -4</p> <p>Therefore, the distance of vertex 3 is -4.</p> <p>Now we move to the second iteration.</p> <p> <strong>Second iteration</strong> </p> <p>Now, again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -4 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-4 + 7) equals to 3 which is less than 4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -4 + 7 = 3</p> <p>Therefore, the value at vertex 2 is 3.</p> <p>The next edge is (2, 4). Since ( 3+7) equals to 10 which is less than 11 so update</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 3 + 7 = 10</p> <p>Therefore, the value at vertex 4 is 10.</p> <p>The next edge is (4, 3). Since (10 - 15) equals to -5 which is less than -4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 10 - 15 = -5</p> <p>Therefore, the value at vertex 3 is -5.</p> <p>Now we move to the third iteration.</p> <p> <strong>Third iteration</strong> </p> <p>Now again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -5 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 which is greater than 3 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-5 + 7) equals to 2 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -5 + 7 = 2</p> <p>Therefore, the value at vertex 2 is 2.</p> <p>The next edge is (2, 4). Since (2 + 7) equals to 9 which is less than 10 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 2 + 7 = 9</p> <p>Therefore, the value at vertex 4 is 9.</p> <p>The next edge is (4, 3). Since (9 - 15) equals to -6 which is less than -5 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 9 - 15 = -6</p> <p>Therefore, the value at vertex 3 is -6.</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-6.webp" alt="Bellman-Ford Algorithm"> <p>Since the graph contains 4 vertices, so according to the bellman ford algorithm, there would be only 3 iterations. If we try to perform 4<sup>th</sup> iteration on the graph, the distance of the vertices from the given vertex should not change. If the distance varies, it means that the bellman ford algorithm is not providing the correct answer.</p> <p> <strong>4<sup>th</sup> iteration</strong> </p> <p>The first edge is (1, 3). Since (0 +5) equals to 5 which is greater than -6 so there would be no change in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) is greater than 2 so there would be no updation.</p> <p>The next edge is (3, 2). Since (-6 + 7) equals to 1 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -6 + 7 = 1</p> <p>In this case, the value of the vertex is updated. So, we conclude that the bellman ford algorithm does not work when the graph contains the negative weight cycle.</p> <p>Therefore, the value at vertex 2 is 1.</p> <hr></-></pre></d(v))>
d(v) = 0 + 6 = 6
Portanto, a distância do vértice B é 6.
Considere a aresta (A, C). Denote o vértice 'A' como 'u' e o vértice 'C' como 'v'. Agora use a fórmula relaxante:
d(você) = 0
d(v) = ∞
c(você, v) = 4
Como (0 + 4) é menor que ∞, atualize
d(v) = d(u) + c(u , v)
d(v) = 0 + 4 = 4
Portanto, a distância do vértice C é 4.
Considere a aresta (A, D). Denote o vértice 'A' como 'u' e o vértice 'D' como 'v'. Agora use a fórmula relaxante:
d(você) = 0
d(v) = ∞
c(você, v) = 5
Como (0 + 5) é menor que ∞, atualize
d(v) = d(u) + c(u , v)
d(v) = 0 + 5 = 5
Portanto, a distância do vértice D é 5.
Considere a aresta (B, E). Denote o vértice 'B' como 'u' e o vértice 'E' como 'v'. Agora use a fórmula relaxante:
d(você) = 6
d(v) = ∞
c(você, v) = -1
Como (6 - 1) é menor que ∞, atualize
d(v) = d(u) + c(u , v)
d(v) = 6 - 1= 5
Portanto, a distância do vértice E é 5.
Considere a aresta (C, E). Denote o vértice 'C' como 'u' e o vértice 'E' como 'v'. Agora use a fórmula relaxante:
d(você) = 4
d(v) = 5
c(você, v) = 3
Como (4 + 3) é maior que 5, não haverá atualização. O valor no vértice E é 5.
Considere a aresta (D, C). Denote o vértice 'D' como 'u' e o vértice 'C' como 'v'. Agora use a fórmula relaxante:
d(você) = 5
d(v) = 4
c(você, v) = -2
Como (5 -2) é menor que 4, atualize
d(v) = d(u) + c(u , v)
d(v) = 5 - 2 = 3
Portanto, a distância do vértice C é 3.
Considere a aresta (D, F). Denote o vértice 'D' como 'u' e o vértice 'F' como 'v'. Agora use a fórmula relaxante:
d(você) = 5
d(v) = ∞
tipos de dados em java
c(você, v) = -1
Como (5 -1) é menor que ∞, então atualize
d(v) = d(u) + c(u , v)
d(v) = 5 - 1 = 4
Portanto, a distância do vértice F é 4.
Considere a aresta (E, F). Denote o vértice 'E' como 'u' e o vértice 'F' como 'v'. Agora use a fórmula relaxante:
d(você) = 5
d(v) = ∞
c(você, v) = 3
Como (5 + 3) é maior que 4, não haveria atualização no valor da distância do vértice F.
Considere a aresta (C, B). Denote o vértice 'C' como 'u' e o vértice 'B' como 'v'. Agora use a fórmula relaxante:
d(você) = 3
d(v) = 6
c(você, v) = -2
Como (3 - 2) é menor que 6, atualize
d(v) = d(u) + c(u , v)
d(v) = 3 - 2 = 1
Portanto, a distância do vértice B é 1.
Agora a primeira iteração está concluída. Passamos para a segunda iteração.
Segunda iteração:
Na segunda iteração, verificamos novamente todas as arestas. A primeira aresta é (A, B). Como (0 + 6) é maior que 1, não haveria atualização no vértice B.
A próxima aresta é (A, C). Como (0 + 4) é maior que 3, não haveria atualização no vértice C.
A próxima aresta é (A, D). Como (0 + 5) é igual a 5, não haveria atualização no vértice D.
A próxima aresta é (B, E). Como (1 - 1) é igual a 0, que é menor que 5, atualize:
d(v) = d(você) + c(você, v)
d(E) = d(B) +c(B, E)
= 1 - 1 = 0
A próxima aresta é (C, E). Como (3 + 3) é igual a 6 que é maior que 5, não haveria atualização no vértice E.
A próxima aresta é (D, C). Como (5 - 2) é igual a 3, não haveria atualização no vértice C.
A próxima aresta é (D, F). Como (5 - 1) é igual a 4, não haveria atualização no vértice F.
A próxima aresta é (E, F). Como (5 + 3) é igual a 8 que é maior que 4, não haveria atualização no vértice F.
A próxima aresta é (C, B). Como (3 - 2) é igual a 1`, não haveria atualização no vértice B.

Terceira iteração
Executaremos as mesmas etapas que fizemos nas iterações anteriores. Observaremos que não haverá atualização na distância dos vértices.
The following are the distances of vertices: A: 0 B: 1 C: 3 D: 5 E: 0 F: 3
Complexidade de tempo
A complexidade de tempo do algoritmo Bellman Ford seria O(E|V| - 1).
function bellmanFord(G, S) for each vertex V in G distance[V] <- 0 infinite previous[v] <- null distance[s] for each vertex v in g edge (u,v) tempdistance distance[u] + edge_weight(u, v) if < distance[v] u distance[v} error: negative cycle exists return distance[], previous[] pre> <p> <strong>Drawbacks of Bellman ford algorithm</strong> </p> <ul> <li>The bellman ford algorithm does not produce a correct answer if the sum of the edges of a cycle is negative. Let's understand this property through an example. Consider the below graph. <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-4.webp" alt="Bellman-Ford Algorithm"></li> <li>In the above graph, we consider vertex 1 as the source vertex and provides 0 value to it. We provide infinity value to other vertices shown as below: <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-5.webp" alt="Bellman-Ford Algorithm"> <br>Edges can be written as: <br> (1, 3), (1, 2), (2, 4), (3, 2), (4, 3) </li> </ul> <p> <strong>First iteration</strong> </p> <p> <strong>Consider the edge (1, 3). Denote vertex '1' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 5</p> <p>Since (0 + 5) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 5 = 5</p> <p>Therefore, the distance of vertex 3 is 5.</p> <p> <strong>Consider the edge (1, 2). Denote vertex '1' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 4</p> <p>Since (0 + 4) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 4 = 4</p> <p>Therefore, the distance of vertex 2 is 4.</p> <p> <strong>Consider the edge (3, 2). Denote vertex '3' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 5</p> <p>d(v) = 4</p> <p>c(u , v) = 7</p> <p>Since (5 + 7) is greater than 4, so there would be no updation in the vertex 2.</p> <p> <strong>Consider the edge (2, 4). Denote vertex '2' as 'u' and vertex '4' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 4</p> <p>d(v) = ∞</p> <p>c(u , v) = 7</p> <p>Since (4 + 7) equals to 11 which is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 4 + 7 = 11</p> <p>Therefore, the distance of vertex 4 is 11.</p> <p> <strong>Consider the edge (4, 3). Denote vertex '4' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 11</p> <p>d(v) = 5</p> <p>c(u , v) = -15</p> <p>Since (11 - 15) equals to -4 which is less than 5, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 11 - 15 = -4</p> <p>Therefore, the distance of vertex 3 is -4.</p> <p>Now we move to the second iteration.</p> <p> <strong>Second iteration</strong> </p> <p>Now, again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -4 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-4 + 7) equals to 3 which is less than 4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -4 + 7 = 3</p> <p>Therefore, the value at vertex 2 is 3.</p> <p>The next edge is (2, 4). Since ( 3+7) equals to 10 which is less than 11 so update</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 3 + 7 = 10</p> <p>Therefore, the value at vertex 4 is 10.</p> <p>The next edge is (4, 3). Since (10 - 15) equals to -5 which is less than -4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 10 - 15 = -5</p> <p>Therefore, the value at vertex 3 is -5.</p> <p>Now we move to the third iteration.</p> <p> <strong>Third iteration</strong> </p> <p>Now again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -5 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 which is greater than 3 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-5 + 7) equals to 2 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -5 + 7 = 2</p> <p>Therefore, the value at vertex 2 is 2.</p> <p>The next edge is (2, 4). Since (2 + 7) equals to 9 which is less than 10 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 2 + 7 = 9</p> <p>Therefore, the value at vertex 4 is 9.</p> <p>The next edge is (4, 3). Since (9 - 15) equals to -6 which is less than -5 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 9 - 15 = -6</p> <p>Therefore, the value at vertex 3 is -6.</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-6.webp" alt="Bellman-Ford Algorithm"> <p>Since the graph contains 4 vertices, so according to the bellman ford algorithm, there would be only 3 iterations. If we try to perform 4<sup>th</sup> iteration on the graph, the distance of the vertices from the given vertex should not change. If the distance varies, it means that the bellman ford algorithm is not providing the correct answer.</p> <p> <strong>4<sup>th</sup> iteration</strong> </p> <p>The first edge is (1, 3). Since (0 +5) equals to 5 which is greater than -6 so there would be no change in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) is greater than 2 so there would be no updation.</p> <p>The next edge is (3, 2). Since (-6 + 7) equals to 1 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -6 + 7 = 1</p> <p>In this case, the value of the vertex is updated. So, we conclude that the bellman ford algorithm does not work when the graph contains the negative weight cycle.</p> <p>Therefore, the value at vertex 2 is 1.</p> <hr></->
d(v) = 0 + 5 = 5
Portanto, a distância do vértice 3 é 5.
Considere a aresta (1, 2). Denote o vértice '1' como 'u' e o vértice '2' como 'v'. Agora use a fórmula relaxante:
d(você) = 0
d(v) = ∞
c(você, v) = 4
Como (0 + 4) é menor que ∞, atualize
d(v) = d(u) + c(u , v)
d(v) = 0 + 4 = 4
Portanto, a distância do vértice 2 é 4.
Considere a aresta (3, 2). Denote o vértice '3' como 'u' e o vértice '2' como 'v'. Agora use a fórmula relaxante:
d(você) = 5
d(v) = 4
c(você, v) = 7
Como (5 + 7) é maior que 4, não haveria atualização no vértice 2.
Considere a aresta (2, 4). Denote o vértice '2' como 'u' e o vértice '4' como 'v'. Agora use a fórmula relaxante:
d(você) = 4
d(v) = ∞
c(você, v) = 7
Como (4 + 7) é igual a 11, que é menor que ∞, então atualize
d(v) = d(u) + c(u , v)
d(v) = 4 + 7 = 11
Portanto, a distância do vértice 4 é 11.
Considere a aresta (4, 3). Denote o vértice '4' como 'u' e o vértice '3' como 'v'. Agora use a fórmula relaxante:
d(você) = 11
d(v) = 5
c(você, v) = -15
Como (11 - 15) é igual a -4, que é menor que 5, então atualize
nome de caracteres especiais
d(v) = d(u) + c(u , v)
d(v) = 11 - 15 = -4
Portanto, a distância do vértice 3 é -4.
Agora passamos para a segunda iteração.
Segunda iteração
Agora, novamente verificaremos todas as arestas. A primeira aresta é (1, 3). Como (0 + 5) é igual a 5 que é maior que -4, não haveria atualização no vértice 3.
A próxima aresta é (1, 2). Como (0 + 4) é igual a 4, não haveria atualização no vértice 2.
A próxima aresta é (3, 2). Como (-4 + 7) é igual a 3, que é menor que 4, atualize:
d(v) = d(você) + c(você, v)
d(2) = d(3) +c(3, 2)
= -4 + 7 = 3
Portanto, o valor no vértice 2 é 3.
A próxima aresta é (2, 4). Como (3+7) é igual a 10, que é menor que 11, então atualize
d(v) = d(você) + c(você, v)
d(4) = d(2) +c(2, 4)
= 3 + 7 = 10
Portanto, o valor no vértice 4 é 10.
mapa java
A próxima aresta é (4, 3). Como (10 - 15) é igual a -5, que é menor que -4, atualize:
d(v) = d(você) + c(você, v)
d(3) = d(4) +c(4, 3)
= 10 - 15 = -5
Portanto, o valor no vértice 3 é -5.
Agora passamos para a terceira iteração.
Terceira iteração
Agora, novamente, verificaremos todas as arestas. A primeira aresta é (1, 3). Como (0 + 5) é igual a 5 que é maior que -5, não haveria atualização no vértice 3.
A próxima aresta é (1, 2). Como (0 + 4) é igual a 4 que é maior que 3, não haveria atualização no vértice 2.
A próxima aresta é (3, 2). Como (-5 + 7) é igual a 2, que é menor que 3, atualize:
d(v) = d(você) + c(você, v)
d(2) = d(3) +c(3, 2)
= -5 + 7 = 2
Portanto, o valor no vértice 2 é 2.
A próxima aresta é (2, 4). Como (2 + 7) é igual a 9, que é menor que 10, atualize:
d(v) = d(você) + c(você, v)
d(4) = d(2) +c(2, 4)
= 2 + 7 = 9
Portanto, o valor no vértice 4 é 9.
A próxima aresta é (4, 3). Como (9 - 15) é igual a -6, que é menor que -5, atualize:
d(v) = d(você) + c(você, v)
d(3) = d(4) +c(4, 3)
= 9 - 15 = -6
Portanto, o valor no vértice 3 é -6.

Como o gráfico contém 4 vértices, de acordo com o algoritmo Bellman Ford, haveria apenas 3 iterações. Se tentarmos realizar 4ºiteração no gráfico, a distância dos vértices do vértice fornecido não deve mudar. Se a distância variar, significa que o algoritmo Bellman Ford não está fornecendo a resposta correta.
4ºiteração
A primeira aresta é (1, 3). Como (0 +5) é igual a 5, que é maior que -6, não haveria alteração no vértice 3.
A próxima aresta é (1, 2). Como (0 + 4) é maior que 2, não haveria atualização.
A próxima aresta é (3, 2). Como (-6 + 7) é igual a 1, que é menor que 3, atualize:
d(v) = d(você) + c(você, v)
d(2) = d(3) +c(3, 2)
= -6 + 7 = 1
Neste caso, o valor do vértice é atualizado. Assim, concluímos que o algoritmo Bellman Ford não funciona quando o gráfico contém o ciclo de peso negativo.
Portanto, o valor no vértice 2 é 1.
