Nesta seção, discutiremos o método de conversão do NFA em seu AFD equivalente. No NFA, quando uma entrada específica é dada ao estado atual, a máquina vai para vários estados. Pode ter zero, um ou mais de um movimento em um determinado símbolo de entrada. Por outro lado, no DFA, quando uma entrada específica é dada ao estado atual, a máquina vai para apenas um estado. O DFA possui apenas um movimento em um determinado símbolo de entrada.
Seja M = (Q, ∑, δ, q0, F) um NFA que aceita a linguagem L(M). Deve haver AFD equivalente denotado por M' = (Q', ∑', q0', δ', F') tal que L(M) = L(M').
Etapas para converter NFA em DFA:
Passo 1: Inicialmente Q' = ϕ
Passo 2: Adicione q0 do NFA a Q'. Em seguida, encontre as transições deste estado inicial.
Etapa 3: Em Q', encontre o conjunto possível de estados para cada símbolo de entrada. Se este conjunto de estados não estiver em Q', adicione-o a Q'.
comprimento da string bash
Passo 4: No DFA, o estado final serão todos os estados que contêm F (estados finais do NFA)
Exemplo 1:
Converta o NFA fornecido em DFA.
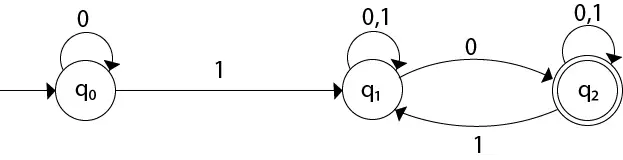
Solução: Para o diagrama de transição fornecido, construiremos primeiro a tabela de transição.
| Estado | 0 | 1 |
|---|---|---|
| →q0 | q0 | q1 |
| q1 | {q1, q2} | q1 |
| *q2 | q2 | {q1, q2} |
Agora obteremos a transição δ' para o estado q0.
regex em java
δ'([q0], 0) = [q0] δ'([q0], 1) = [q1]
A transição δ' para o estado q1 é obtida como:
δ'([q1], 0) = [q1, q2] (new state generated) δ'([q1], 1) = [q1]
A transição δ' para o estado q2 é obtida como:
δ'([q2], 0) = [q2] δ'([q2], 1) = [q1, q2]
Agora obteremos a transição δ' em [q1, q2].
δ'([q1, q2], 0) = δ(q1, 0) ∪ δ(q2, 0) = {q1, q2} ∪ {q2} = [q1, q2] δ'([q1, q2], 1) = δ(q1, 1) ∪ δ(q2, 1) = {q1} ∪ {q1, q2} = {q1, q2} = [q1, q2] O estado [q1, q2] também é o estado final porque contém um estado final q2. A tabela de transição para o DFA construído será:
índice java de
| Estado | 0 | 1 |
|---|---|---|
| →[q0] | [q0] | [q1] |
| [q1] | [q1, q2] | [q1] |
| *[q2] | [q2] | [q1, q2] |
| *[q1, q2] | [q1, q2] | [q1, q2] |
O diagrama de transição será:

O estado q2 pode ser eliminado porque q2 é um estado inacessível.
Exemplo 2:
Converta o NFA fornecido em DFA.

Solução: Para o diagrama de transição fornecido, construiremos primeiro a tabela de transição.
string java de array
| Estado | 0 | 1 |
|---|---|---|
| →q0 | {q0, q1} | {q1} |
| *q1 | ϕ | {q0, q1} |
Agora obteremos a transição δ' para o estado q0.
δ'([q0], 0) = {q0, q1} = [q0, q1] (new state generated) δ'([q0], 1) = {q1} = [q1] A transição δ' para o estado q1 é obtida como:
δ'([q1], 0) = ϕ δ'([q1], 1) = [q0, q1]
Agora obteremos a transição δ' em [q0, q1].
δ'([q0, q1], 0) = δ(q0, 0) ∪ δ(q1, 0) = {q0, q1} ∪ ϕ = {q0, q1} = [q0, q1] De forma similar,
δ'([q0, q1], 1) = δ(q0, 1) ∪ δ(q1, 1) = {q1} ∪ {q0, q1} = {q0, q1} = [q0, q1] Como no NFA fornecido, q1 é um estado final, então no AFD, onde quer que exista q1, esse estado se torna um estado final. Portanto, no AFD, os estados finais são [q1] e [q0, q1]. Portanto conjunto de estados finais F = {[q1], [q0, q1]}.
A tabela de transição para o DFA construído será:
| Estado | 0 | 1 |
|---|---|---|
| →[q0] | [q0, q1] | [q1] |
| *[q1] | ϕ | [q0, q1] |
| *[q0, q1] | [q0, q1] | [q0, q1] |
O diagrama de transição será:
string para int java

Até nós podemos mudar o nome dos estados do DFA.
Suponha
A = [q0] B = [q1] C = [q0, q1]
Com esses novos nomes o DFA será o seguinte:

