O método ganancioso é uma das estratégias como Dividir para conquistar usada para resolver os problemas. Este método é usado para resolver problemas de otimização. Um problema de otimização é um problema que exige resultados máximos ou mínimos. Vamos entender através de alguns termos.

O método Greedy é a abordagem mais simples e direta. Não é um algoritmo, mas é uma técnica. A principal função desta abordagem é que a decisão seja tomada com base nas informações atualmente disponíveis. Qualquer que seja a informação atual presente, a decisão é tomada sem preocupação com o efeito da decisão atual no futuro.

ator ekta kapoor

Esta técnica é usada basicamente para determinar a solução viável que pode ou não ser ótima. A solução viável é um subconjunto que satisfaz os critérios fornecidos. A solução ótima é aquela que é a melhor e mais favorável solução no subconjunto. No caso de viável, se mais de uma solução satisfizer os critérios determinados então essas soluções serão consideradas viáveis, enquanto a solução ótima é a melhor solução entre todas as soluções.

Características do método ganancioso

A seguir estão as características de um método ganancioso:

• Para construir a solução de forma ótima, este algoritmo cria dois conjuntos onde um conjunto contém todos os itens escolhidos e outro conjunto contém os itens rejeitados.
• Um algoritmo Greedy faz boas escolhas locais na esperança de que a solução seja viável ou ótima.

Componentes do algoritmo ganancioso

Os componentes que podem ser usados ​​no algoritmo guloso são:

classificação de inserção java

Conjunto de candidatos:Uma solução criada a partir do conjunto é conhecida como conjunto candidato.Função de seleção:Esta função é usada para escolher o candidato ou subconjunto que pode ser adicionado na solução.Função de viabilidade:Uma função usada para determinar se o candidato ou subconjunto pode ser usado para contribuir para a solução ou não.Função objetiva:Uma função é usada para atribuir o valor à solução ou à solução parcial.Função de solução:Esta função é usada para informar se a função completa foi alcançada ou não.

Aplicações do algoritmo ganancioso

• É usado para encontrar o caminho mais curto.
• É usado para encontrar a árvore geradora mínima usando o algoritmo do prim ou o algoritmo de Kruskal.
• É utilizado em um sequenciamento de trabalhos com prazo.
• Este algoritmo também é usado para resolver o problema da mochila fracionária.

Pseudocódigo do algoritmo ganancioso

 Algorithm Greedy (a, n) { Solution : = 0; for i = 0 to n do { x: = select(a); if feasible(solution, x) { Solution: = union(solution , x) } return solution; } } 

O acima é o algoritmo ganancioso. Inicialmente, a solução recebe valor zero. Passamos o array e o número de elementos no algoritmo ganancioso. Dentro do loop for, selecionamos o elemento um por um e verificamos se a solução é viável ou não. Se a solução for viável, então realizamos a união.

Vamos entender através de um exemplo.

Suponha que haja um problema 'P'. Quero viajar de A para B mostrado abaixo:

P: A → B

O problema é que temos que percorrer esta viagem de A a B. Existem várias soluções para ir de A a B. Podemos ir de A a B por andar, carro, bicicleta, trem, avião , etc. Há uma restrição na jornada de que temos que percorrê-la dentro de 12 horas. Se eu for de trem ou avião, só então posso cobrir essa distância em 12 horas. Existem muitas soluções para este problema, mas existem apenas duas soluções que satisfazem a restrição.

'fórmula do pedreiro'

Se dissermos que temos que cobrir a viagem com o custo mínimo. Isso significa que temos que percorrer essa distância o mínimo possível, por isso esse problema é conhecido como problema de minimização. Até agora, temos duas soluções viáveis, ou seja, uma de trem e outra de avião. Como viajar de trem terá um custo mínimo, é uma solução ideal. Uma solução ótima também é a solução viável, mas fornece o melhor resultado para que essa solução seja a solução ótima com o custo mínimo. Haveria apenas uma solução ótima.

O problema que requer resultado mínimo ou máximo é conhecido como problema de otimização. O método guloso é uma das estratégias utilizadas para resolver os problemas de otimização.

Desvantagens de usar o algoritmo Greedy

O algoritmo ganancioso toma decisões com base nas informações disponíveis em cada fase, sem considerar o problema mais amplo. Portanto, pode haver a possibilidade de que a solução gananciosa não forneça a melhor solução para todos os problemas.

Segue a escolha do ótimo local em cada estágio com a intenção de encontrar o ótimo global. Vamos entender através de um exemplo.

Considere o gráfico abaixo:

pandas criando dataframe

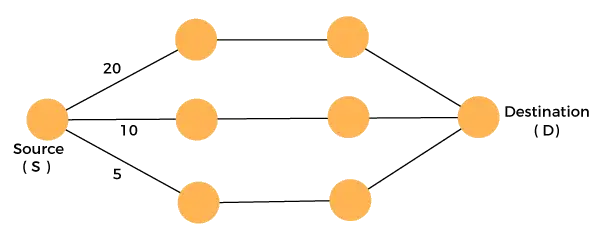
Temos que viajar da origem ao destino com o custo mínimo. Como temos três soluções viáveis ​​com caminhos de custo 10, 20 e 5. 5 é o caminho de custo mínimo, portanto é a solução ideal. Este é o ótimo local e, desta forma, encontramos o ótimo local em cada etapa para calcular a solução ótima global.