O que é pilha?
Um heap é uma árvore binária completa, e a árvore binária é uma árvore na qual o nó pode ter no máximo dois filhos. Antes de saber mais sobre heap O que é uma árvore binária completa?
Uma árvore binária completa é um árvore binária na qual todos os níveis, exceto o último nível, ou seja, o nó folha, devem ser completamente preenchidos e todos os nós devem ser justificados à esquerda.
Vamos entender através de um exemplo.
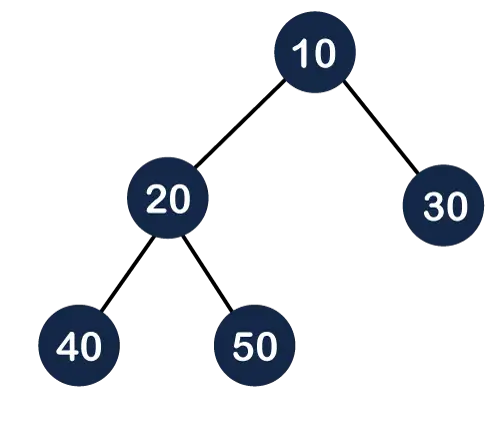
Na figura acima, podemos observar que todos os nós internos estão completamente preenchidos, exceto o nó folha; portanto, podemos dizer que a árvore acima é uma árvore binária completa.

A figura acima mostra que todos os nós internos estão completamente preenchidos, exceto o nó folha, mas os nós folha são adicionados na parte direita; portanto, a árvore acima não é uma árvore binária completa.
Nota: A árvore heap é uma estrutura de dados de árvore binária balanceada especial onde o nó raiz é comparado com seus filhos e organizado de acordo.
Como podemos organizar os nós na árvore?
Existem dois tipos de heap:
- Pilha mínima
- Pilha máxima
Pilha mínima: O valor do nó pai deve ser menor ou igual a qualquer um de seus filhos.
Ou
Em outras palavras, o min-heap pode ser definido como, para cada nó i, o valor do nó i é maior ou igual ao seu valor pai, exceto o nó raiz. Matematicamente, pode ser definido como:
Um[pai(a)]<= a[i]< strong>
Vamos entender o min-heap através de um exemplo.

Na figura acima, 11 é o nó raiz e o valor do nó raiz é menor que o valor de todos os outros nós (filho esquerdo ou filho direito).
Pilha máxima: O valor do nó pai é maior ou igual ao de seus filhos.
Ou
Em outras palavras, o heap máximo pode ser definido para cada nó i; o valor do nó i é menor ou igual ao seu valor pai, exceto o nó raiz. Matematicamente, pode ser definido como:
caractere de escape java
A[Pai(i)] >= A[i]

A árvore acima é uma árvore de heap máximo, pois satisfaz a propriedade do heap máximo. Agora, vamos ver a representação do array do heap máximo.
Complexidade de tempo no Max Heap
O número total de comparações necessárias no heap máximo depende da altura da árvore. A altura da árvore binária completa é sempre logn; portanto, a complexidade do tempo também seria O(logn).
Algoritmo de operação de inserção no heap máximo.
// algorithm to insert an element in the max heap. insertHeap(A, n, value) { n=n+1; // n is incremented to insert the new element A[n]=value; // assign new value at the nth position i = n; // assign the value of n to i // loop will be executed until i becomes 1. while(i>1) { parent= floor value of i/2; // Calculating the floor value of i/2 // Condition to check whether the value of parent is less than the given node or not if(A[parent] <a[i]) { swap(a[parent], a[i]); i="parent;" } else return; < pre> <p> <strong>Let's understand the max heap through an example</strong> .</p> <p>In the above figure, 55 is the parent node and it is greater than both of its child, and 11 is the parent of 9 and 8, so 11 is also greater than from both of its child. Therefore, we can say that the above tree is a max heap tree.</p> <p> <strong>Insertion in the Heap tree</strong> </p> <p> <strong>44, 33, 77, 11, 55, 88, 66</strong> </p> <p>Suppose we want to create the max heap tree. To create the max heap tree, we need to consider the following two cases:</p> <ul> <li>First, we have to insert the element in such a way that the property of the complete binary tree must be maintained.</li> <li>Secondly, the value of the parent node should be greater than the either of its child.</li> </ul> <p> <strong>Step 1:</strong> First we add the 44 element in the tree as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-5.webp" alt="Heap Data Structure"> <p> <strong>Step 2:</strong> The next element is 33. As we know that insertion in the binary tree always starts from the left side so 44 will be added at the left of 33 as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-6.webp" alt="Heap Data Structure"> <p> <strong>Step 3:</strong> The next element is 77 and it will be added to the right of the 44 as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-7.webp" alt="Heap Data Structure"> <p>As we can observe in the above tree that it does not satisfy the max heap property, i.e., parent node 44 is less than the child 77. So, we will swap these two values as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-8.webp" alt="Heap Data Structure"> <p> <strong>Step 4:</strong> The next element is 11. The node 11 is added to the left of 33 as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-9.webp" alt="Heap Data Structure"> <p> <strong>Step 5:</strong> The next element is 55. To make it a complete binary tree, we will add the node 55 to the right of 33 as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-10.webp" alt="Heap Data Structure"> <p>As we can observe in the above figure that it does not satisfy the property of the max heap because 33<55, so we will swap these two values as shown below:< p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-11.webp" alt="Heap Data Structure"> <p> <strong>Step 6:</strong> The next element is 88. The left subtree is completed so we will add 88 to the left of 44 as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-12.webp" alt="Heap Data Structure"> <p>As we can observe in the above figure that it does not satisfy the property of the max heap because 44<88, so we will swap these two values as shown below:< p> <p>Again, it is violating the max heap property because 88>77 so we will swap these two values as shown below:</p> <p> <strong>Step 7:</strong> The next element is 66. To make a complete binary tree, we will add the 66 element to the right side of 77 as shown below:</p> <p>In the above figure, we can observe that the tree satisfies the property of max heap; therefore, it is a heap tree.</p> <p> <strong>Deletion in Heap Tree</strong> </p> <p>In Deletion in the heap tree, the root node is always deleted and it is replaced with the last element.</p> <p> <strong>Let's understand the deletion through an example.</strong> </p> <p> <strong>Step 1</strong> : In the above tree, the first 30 node is deleted from the tree and it is replaced with the 15 element as shown below:</p> <p>Now we will heapify the tree. We will check whether the 15 is greater than either of its child or not. 15 is less than 20 so we will swap these two values as shown below:</p> <p>Again, we will compare 15 with its child. Since 15 is greater than 10 so no swapping will occur.</p> <p> <strong>Algorithm to heapify the tree</strong> </p> <pre> MaxHeapify(A, n, i) { int largest =i; int l= 2i; int r= 2i+1; while(lA[largest]) { largest=l; } while(rA[largest]) { largest=r; } if(largest!=i) { swap(A[largest], A[i]); heapify(A, n, largest); }} </pre> <hr></88,></p></55,></p></a[i])> 