A altura ou profundidade de uma árvore binária pode ser definida como o máximo ou o maior número de arestas de um nó folha ao nó raiz ou do nó raiz ao nó folha. O nó raiz estará no nível zero, o que significa que se o nó raiz não tiver nenhum dos nós filhos conectados a ele, a altura ou profundidade da árvore binária específica será considerada zero.
Tomemos um exemplo para uma melhor compreensão da altura da árvore binária.
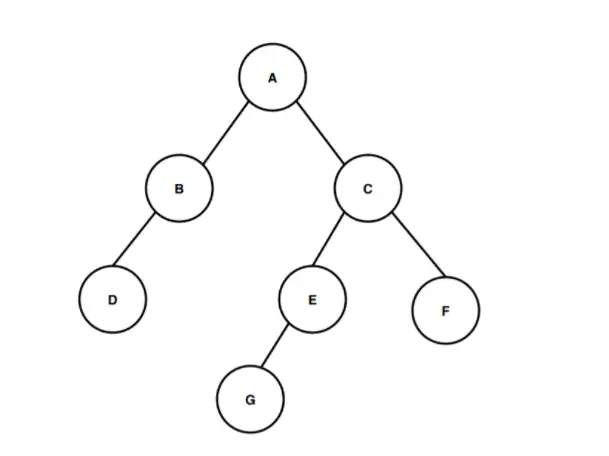
Na imagem acima, temos uma árvore binária começando no nó raiz chamado A. O nó raiz A tem dois nós filhos B e C como filho esquerdo e filho direito, respectivamente. E da mesma forma, o nó filho esquerdo B tem apenas um nó filho esquerdo chamado D e o nó filho direito C tem dois nós filhos E e F, dos quais o nó E tem o nó G como o único filho esquerdo.
nova linha python
Agora vamos calcular a altura desta árvore binária. Conte o número de arestas começando do nó raiz até o nó folha mais profundo para calcular a altura da árvore binária. O nó mais profundo que está presente nesta árvore binária é o nó G. Portanto, para o cálculo da altura ou profundidade desta árvore binária precisamos calcular o número de arestas entre o nó raiz e o nó mais profundo G. A primeira aresta é do nó A ao nó C, a segunda aresta é do nó C ao nó E e a terceira aresta é do nó E ao nó G. Portanto, para percorrer do nó raiz A ao nó mais profundo G, existem três arestas , então a altura ou profundidade da árvore binária é 3. O caminho que seguimos para passar da raiz ao nó folha mais profundo é A > C > E > G e este caminho cobre três arestas durante a travessia, é por isso que de acordo para a definição da altura da árvore binária, a altura desta árvore binária é 3.
Maneiras de encontrar a altura da árvore binária
Agora, vamos escrever um código para encontrar a altura de uma árvore binária. Existem duas maneiras de encontrar a altura da árvore binária. Um é o método recursivo e o outro é o método não recursivo que fará uso da estrutura de dados Queue para calcular a altura da árvore binária.
Maneira Recursiva
Primeiro, vamos ver a maneira recursiva de encontrar a altura da árvore binária.
Código:
// Java program to create and to find the height of a binary tree by recursive way // util package is imported to use classes like Queue and LinkedList import java.util.*; // A class named Node is created representing a single node of a binary tree class Node{ // The class Node has three class variables named key and left and right of int type and Node type respectively. // the key variable holds the actual value that is assigned to that node of the binary tree int key; // left and right variables that are of Node type will be used to store the left and right child nodes of the parent of the binary tree Node left, right; // a parameterized constructor is created to create and add data to the node at the same time. public Node(int item) { key = item; left = right = null; } } // end of node class definition // A public class named BinaryTree is created having two constructors and methods to print the binary tree level-wise. class BinaryTree{ // A static variable named root_node is created that will represent the node of the binary tree static Node root_node; // A parametrized constructor of the BinaryTree class is written having the key as a parameter BinaryTree(int key) { // here we are constructing a new node and assigning it to the root node root_node = new Node(key); } BinaryTree() { root_node = null; } // a public static function named print tree is created to print all the nodes in the tree level-wise starting from the root node public static void printTree() { int h = height(root_node); int i; for (i=1; i<=h; i++){ printcurrentlevel(root_node, i); system.out.println(); } a public static function named height is created to fund the of binary tree starting from root node deepest leaf that present in passed as parameter called recursively until returned null find int height(node root){ then will be zero if (root="=" null) return 0; else { * compute each subtree lheight="height(root.left);" rheight="height(root.right);" use larger one both sub trees calcualted and which higher used. (lheight> rheight) return(lheight+1); else return(rheight+1); } } // a Public static function named printCurrentLevel is created to print al the nodes that are present in that level // this function is called repeatedly for each level of the binary tree to print all the nodes in that particular level public static void printCurrentLevel (Node root ,int level) { if (root == null) return; if (level == 1) System.out.print(root.key + ' '); else if (level > 1) { printCurrentLevel(root.left, level-1); printCurrentLevel(root.right, level-1); } } //the main function is created to create an object of the BinaryTree class and call the printTree method to level-wise print the nodes of the binary tree and the height method to find the height of the binary tree public static void main(String[] args){ // first of all we have created an Object of the BinaryTree class that will represent the binary tree BinaryTree tree = new BinaryTree(); // now a new node with the value as 150 is added as the root node to the Binary Tree tree.root_node = new Node(150); // now a new node with the value 250 is added as a left child to the root node tree.root_node.left = new Node(250); // now a new node with the value 270 is added as a right child to the root node tree.root_node.right = new Node(270); // now a new node with the value 320 is added as a left child to the left node of the previous level node tree.root_node.left.left = new Node(320); // now a new node with the value 350 is added as a right child to the right node of the previous level node tree.root_node.left.right = new Node(350); /* 150 / 250 270 / / 320 350 null null */ System.out.println('Printing the nodes of tree level wise :'); System.out.println('Level order traversal : '); tree.printTree(); // height of the binary tree is calculated bypassing the root as parameter to the height() function. int h = tree.height(tree.root_node) System.out.println('The height of the Binary tree is : ' + h ); } } // end of the BinaryTree class </=h;> Saída: A saída do código acima é:
Printing the nodes of tree level wise: Level order traversal: (level 0) 150 (level 1) 250 270 (level 2) 320 350 The height of the Binary tree is: 2
De forma recursiva, chamamos o altura() função repetidamente para encontrar a altura da árvore binária. O nó raiz da árvore binária é passado como parâmetro para a função height(). A função height() calcula a altura de ambas as subárvores do nó raiz e qual entre as duas alturas é maior é considerada a altura da árvore binária.
olá mundo java
Maneira Não Recursiva
Agora vamos ver a maneira não recursiva de encontrar a altura da árvore binária.
Código:
// A C++ program to create and to find the height of a binary tree by non recursive way // iostream header file is included to use the cin and cout objects of the istream and ostream classes respectively #include #include using namespace std; // A struct named Node is created representing a single node of a binary tree struct Node { // The struct Node has three variables named key and left and right of int type and Node type respectively. // the key variable holds the actual value that is assigned to that node of the binary tree int key; // left and right variables that are of Node type will be used to store the left and right child nodes of the parent of the binary tree struct Node* left, *right; }; // A Function named newNode is created to add a new node to the binary tree, the newNode function has one parameter of integer type named key that will represent the value that particular new node will be storing Node* newNode(int key) { Node* temp = new Node; temp->key = key; temp->left = temp->right = NULL; return (temp); } // A function named height is created to find the height of the binary tree with non recursive way // The parameter to the height function is the root node of the binary tree that will be present at level zero // In the height function the nodes of the binary tree are added into the Queue data structure and the depth variable is incremented until // the NULL node is encountered while traversing the nodes of the binary tree stored in the Queue data structure. int height(struct Node* root){ //Initialising a variable to count the //height of tree int depth = 0; queueq; //Pushing first level element along with NULL q.push(root); q.push(NULL); while(!q.empty()){ Node* temp = q.front(); q.pop(); //When NULL encountered, increment the value if(temp == NULL){ depth++; } //If NULL not encountered, keep moving if(temp != NULL){ if(temp->left){ q.push(temp->left); } if(temp->right){ q.push(temp->right); } } //If queue still have elements left, //push NULL again to the queue. else if(!q.empty()){ q.push(NULL); } } return depth; } // Start of the main function int main() { // first of all we have created an Object of the struct Node that will represent the binary tree // the value of the root node is 10 Node *root = newNode(10); // now a new node with the value 20 is added as a left child to the root node root->left = newNode(20); // now a new node with the value 30 is added as a right child to the root node root->right = newNode(30); // now a new node with the value 40 is added as a left child to the left node of the previous level node root->left->left = newNode(40); // now a new node with the value 50 is added as a right child to the left node of the previous level node root->left->right = newNode(50); /* 10 / 20 30 / / 40 50 null null */ cout<<'the height(depth) of tree is: '<<height(root); cout<<endl; } end the main function < pre> <p> <strong>Output:</strong> </p> <pre> The Height(Depth) of the tree is: 2 </pre> <p>In this approach, we have used a non recursive way to find the depth of the binary tree. To find the height of the binary tree, we have written a function named height that will require a parameter of Node type (that means the root of the binary tree whose height needs to be calculated). The root of the binary tree is present at level zero, which means the height or depth of the root is zero.</p> <p>In the non recursive approach, we use the Queue Data Structure to find the depth of the binary tree. The nodes of the binary tree for which we want to find the depth are added to the Queue data structure with the help of an enqueue operation to which the node of the binary tree is passed as a parameter to this function.</p> <p>Once all the nodes are added to the queue, the nodes added in the queue are removed by calling the dequeue function that will keep on removing one element from the queue until the null node of the binary tree is encountered. Each time a node of the binary tree from the queue is removed, the depth variable representing the depth of the binary tree is incremented by one. And in the end, the value of the depth variable will represent the final depth of the binary tree.</p> <hr></'the> Nesta abordagem, usamos uma forma não recursiva para encontrar a profundidade da árvore binária. Para encontrar a altura da árvore binária, escrevemos uma função chamada height que exigirá um parâmetro do tipo Node (que significa a raiz da árvore binária cuja altura precisa ser calculada). A raiz da árvore binária está presente no nível zero, o que significa que a altura ou profundidade da raiz é zero.
Na abordagem não recursiva, usamos a Estrutura de Dados da Fila para encontrar a profundidade da árvore binária. Os nós da árvore binária para os quais queremos encontrar a profundidade são adicionados à estrutura de dados Queue com a ajuda de uma operação de enfileiramento para a qual o nó da árvore binária é passado como parâmetro para esta função.
Depois que todos os nós são adicionados à fila, os nós adicionados na fila são removidos chamando a função de desenfileiramento que continuará removendo um elemento da fila até que o nó nulo da árvore binária seja encontrado. Cada vez que um nó da árvore binária da fila é removido, a variável de profundidade que representa a profundidade da árvore binária é incrementada em um. E no final, o valor da variável profundidade representará a profundidade final da árvore binária.
