Neste artigo, discutiremos a travessia pós-ordem na estrutura de dados.
Estruturas de dados lineares, como pilha, array, fila, etc., só têm uma maneira de percorrer os dados. Mas em uma estrutura de dados hierárquica como árvore , existem várias maneiras de percorrer os dados. Portanto, discutiremos aqui outra maneira de percorrer a estrutura de dados em árvore, ou seja, passagem de pedidos por correio . O percurso pós-ordem é uma das técnicas de percurso utilizadas para visitar o nó da árvore. Segue o princípio LRN (nó esquerdo-direito) . A travessia pós-ordem é usada para obter a expressão pós-fixada de uma árvore.
que meses são o primeiro trimestre
As etapas a seguir são usadas para realizar o percurso pós-ordem:
- Percorra a subárvore esquerda chamando a função de pós-ordem recursivamente.
- Percorra a subárvore direita chamando a função de pós-ordem recursivamente.
- Acesse a parte de dados do nó atual.
A técnica de travessia de pós-ordem segue o Raiz Esquerda Direita política. Aqui, Raiz Esquerda Direita significa que a subárvore esquerda do nó raiz é percorrida primeiro, depois a subárvore direita e, finalmente, o nó raiz é percorrido. Aqui, o próprio nome Postorder sugere que o nó raiz da árvore seria finalmente percorrido.
Algoritmo
Agora, vamos ver o algoritmo de travessia pós-ordem.
Step 1: Repeat Steps 2 to 4 while TREE != NULL Step 2: POSTORDER(TREE -> LEFT) Step 3: POSTORDER(TREE -> RIGHT) Step 4: Write TREE -> DATA [END OF LOOP] Step 5: END
Exemplo de passagem de pedido por correio
Agora, vamos ver um exemplo de travessia pós-ordem. Será mais fácil entender o processo de travessia pós-ordem usando um exemplo.
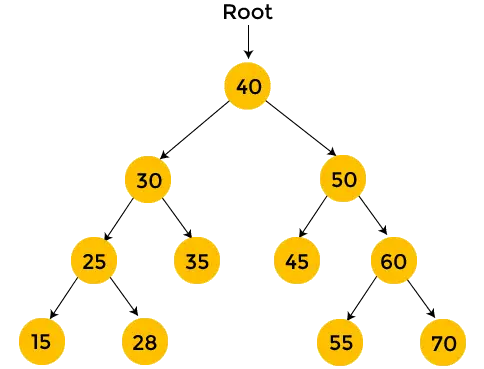
Os nós com cor amarela ainda não foram visitados. Agora, percorreremos os nós da árvore acima usando travessia pós-ordem.
- Aqui, 40 é o nó raiz. Primeiro visitamos a subárvore esquerda de 40, ou seja, 30. O nó 30 também percorrerá em pós-ordem. 25 é a subárvore esquerda de 30, portanto também é percorrida na pós-ordem. Então 15 é a subárvore esquerda de 25. Mas 15 não tem subárvore, então imprimir 15 e vá em direção à subárvore direita de 25.
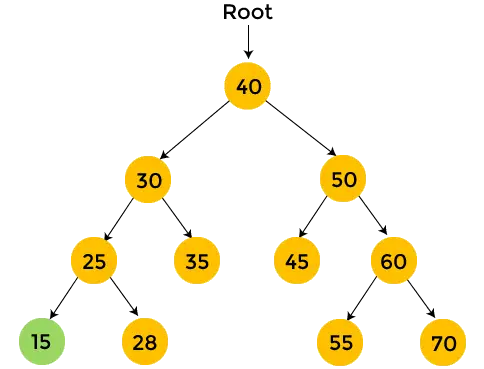
- 28 é a subárvore correta de 25 e não tem filhos. Então, imprimir 28 .
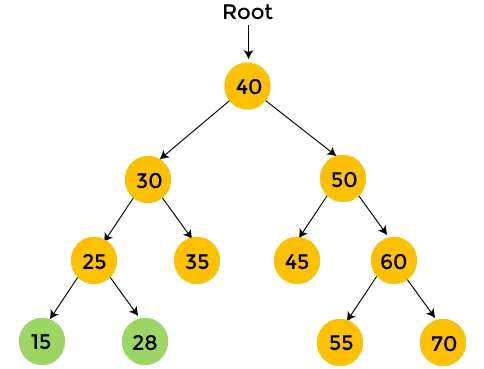
- Agora, imprimir 25 , e o percurso pós-ordem para 25 está terminado.
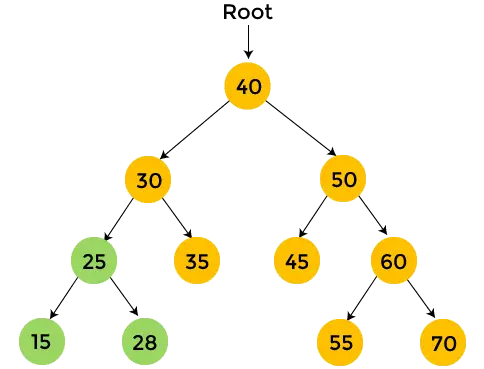
- Em seguida, vá em direção à subárvore direita de 30. 35 é a subárvore direita de 30 e não tem filhos. Então, imprimir 35 .
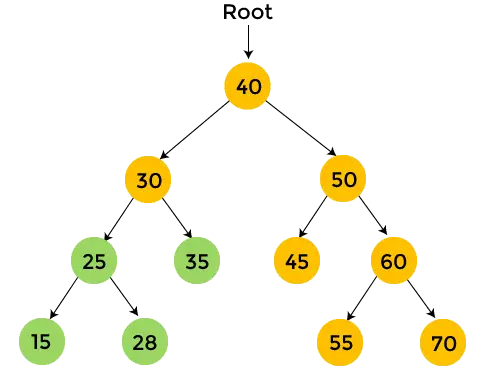
- Depois disso, imprimir 30 , e o percurso pós-ordem para 30 está terminado. Portanto, a subárvore esquerda de determinada árvore binária é percorrida.
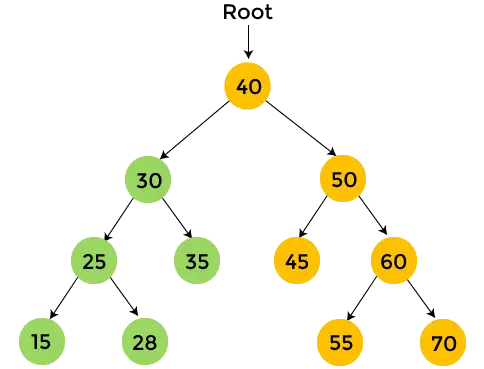
- Agora, vá em direção à subárvore direita de 40 que é 50, e ela também percorrerá a ordem posterior. 45 é a subárvore esquerda de 50 e não tem filhos. Então, imprimir 45 e vá em direção à subárvore direita de 50.
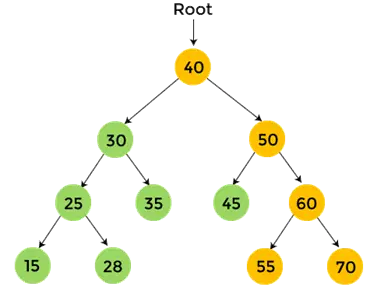
- 60 é a subárvore direita de 50, que também será percorrida na pós-ordem. 55 é a subárvore esquerda de 60 que não tem filhos. Então, imprimir 55 .
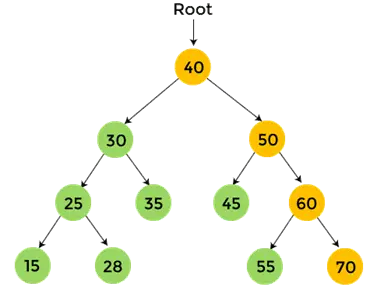
- Agora, imprimir 70, que é a subárvore direita de 60.
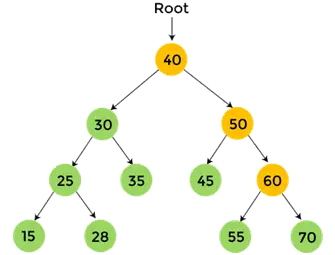
- Agora, imprimir 60, e o percurso de pós-ordem para 60 é concluído.
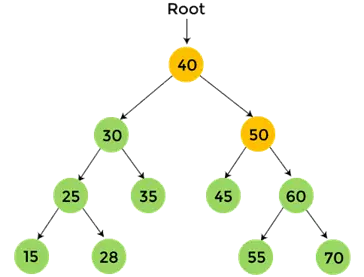
- Agora, imprimir 50, e o percurso de pós-ordem para 50 é concluído.
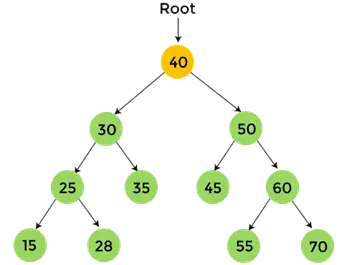
- Afinal, imprimir 40, que é o nó raiz da árvore binária fornecida, e a travessia de pós-ordem para o nó 40 é concluída.
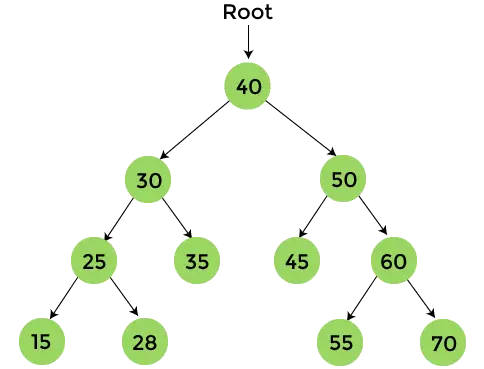
A saída final que obteremos após a travessia pós-ordem é -
{15, 28, 25, 35, 30, 45, 55, 70, 60, 50, 40}
Complexidade da passagem de pedidos por correio
A complexidade de tempo da travessia pós-ordem é Sobre) , onde 'n' é o tamanho da árvore binária.
Considerando que a complexidade espacial da travessia pós-ordem é O(1) , se não considerarmos o tamanho da pilha para chamadas de função. Caso contrário, a complexidade espacial da travessia pós-ordem é Oh) , onde 'h' é a altura da árvore.
Implementação de travessia de pedidos por correio
Agora, vamos ver a implementação do percurso pós-ordem em diferentes linguagens de programação.
Programa: Escreva um programa para implementar travessia pós-ordem em linguagem C.
#include #include struct node { s struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in postorder*/ void traversePostorder(struct node* root) { if (root == NULL) return; traversePostorder(root->left); traversePostorder(root->right); printf(' %d ', root->element); } int main() { struct node* root = createNode(40); root->left = createNode(30); root->right = createNode(50); root->left->left = createNode(25); root->left->right = createNode(35); root->left->left->left = createNode(15); root->left->left->right = createNode(28); root->right->left = createNode(45); root->right->right = createNode(60); root->right->right->left = createNode(55); root->right->right->right = createNode(70); printf('
The Postorder traversal of given binary tree is -
'); traversePostorder(root); return 0; } Saída
truncar e excluir diferença

Programa: Escreva um programa para implementar travessia pós-ordem em C++.
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in postorder*/ void traversePostorder(struct node* root) { if (root == NULL) return; traversePostorder(root->left); traversePostorder(root->right); cout<<' '<element<left="createNode(28);" root->right = createNode(48); root->left->left = createNode(23); root->left->right = createNode(33); root->left->left->left = createNode(13); root->left->left->right = createNode(26); root->right->left = createNode(43); root->right->right = createNode(58); root->right->right->left = createNode(53); root->right->right->right = createNode(68); cout<<'
the postorder traversal of given binary tree is -
'; traversepostorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/85/postorder-traversal-14.webp" alt="Postorder Traversal"> <p> <strong>Program:</strong> Write a program to implement postorder traversal in C#.</p> <pre> using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); Console.Write(node.value + ' '); } void traversePostorder() { traversePostorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(37); bt.root.left = new Node(27); bt.root.right = new Node(47); bt.root.left.left = new Node(22); bt.root.left.right = new Node(32); bt.root.left.left.left = new Node(12); bt.root.left.left.right = new Node(25); bt.root.right.left = new Node(42); bt.root.right.right = new Node(57); bt.root.right.right.left = new Node(52); bt.root.right.right.right = new Node(67); Console.WriteLine('The Postorder traversal of given binary tree is - '); bt.traversePostorder(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/85/postorder-traversal-15.webp" alt="Postorder Traversal"> <p> <strong>Program:</strong> Write a program to implement postorder traversal in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class PostorderTraversal { Node root; PostorderTraversal() { root = null; } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); System.out.print(node.value + ' '); } void traversePostorder() { traversePostorder(root); } public static void main(String args[]) { PostorderTraversal pt = new PostorderTraversal(); pt.root = new Node(36); pt.root.left = new Node(26); pt.root.right = new Node(46); pt.root.left.left = new Node(21); pt.root.left.right = new Node(31); pt.root.left.left.left = new Node(11); pt.root.left.left.right = new Node(24); pt.root.right.left = new Node(41); pt.root.right.right = new Node(56); pt.root.right.right.left = new Node(51); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Postorder traversal of given binary tree is - '); pt.traversePostorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/85/postorder-traversal-16.webp" alt="Postorder Traversal"> <p>So, that's all about the article. Hope the article will be helpful and informative to you.</p> <hr></'
></'> Saída
Após a execução do código acima, a saída será -

Programa: Escreva um programa para implementar travessia pós-ordem em Java.
class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class PostorderTraversal { Node root; PostorderTraversal() { root = null; } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); System.out.print(node.value + ' '); } void traversePostorder() { traversePostorder(root); } public static void main(String args[]) { PostorderTraversal pt = new PostorderTraversal(); pt.root = new Node(36); pt.root.left = new Node(26); pt.root.right = new Node(46); pt.root.left.left = new Node(21); pt.root.left.right = new Node(31); pt.root.left.left.left = new Node(11); pt.root.left.left.right = new Node(24); pt.root.right.left = new Node(41); pt.root.right.right = new Node(56); pt.root.right.right.left = new Node(51); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Postorder traversal of given binary tree is - '); pt.traversePostorder(); System.out.println(); } } Saída
Após a execução do código acima, a saída será -

Então, isso é tudo sobre o artigo. Espero que o artigo seja útil e informativo para você.











