A porcentagem é um conceito fundamental da matemática que não é importante apenas na matemática, mas também em nossa vida diária. Ajuda-nos a expressar frações e proporções de forma simples, facilitando a comparação e a compreensão desses valores. Um dos exemplos comuns que surgem em muitos cenários é o cálculo de 30 por cento, então, neste artigo, conheceremos o conceito de 30 por cento, entenderemos o 30 por cento de 100, e conheça as aplicações e conclusão no final.
Compreendendo as porcentagens
Antes de aprendermos sobre o cálculo de 30% de 100, vamos garantir que temos um bom conhecimento do conceito de percentagens. Uma porcentagem é uma forma de expressar uma proporção ou fração de 100. O símbolo '%' representa uma porcentagem e é lido como ' por cento .' As porcentagens são comumente usadas para comparar valores e fazer declarações relativas.
java converte string para int
Calculando 30% de 100
Para calcular 30 por cento de 100, precisamos de seguir um processo simples. Como '30%' significa 30 de 100, podemos expressá-lo como uma fração: 30/100. Para encontrar 30% de 100, multiplique a fração 30/100 por 100.
Vamos analisar o cálculo passo a passo
Aprenderemos como calcular 30% de 100 com a ajuda de alguns passos simples, que serão explicados nas linhas a seguir.
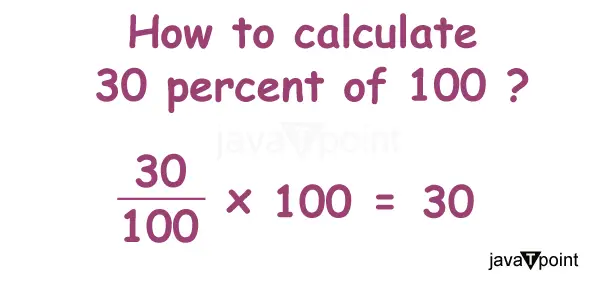
Passo 1 . Primeiro, escreva o produto de ambos os números, ou seja, 30% e 100, conforme mostrado abaixo.
= 30% * 100
Passo 2 . Como sabemos, o significado de porcentagem é 100ºparte de um número ou qualquer coisa para que possamos substituir o '%' por (1/100).
= 30% * 100 = (30/100) * 100
etapa 3 . Usando as regras de multiplicação e simplificação, obtemos o seguinte:
=30% * 100 = (30/100) * 100
= 3.000/100
= 30
Aplicações de porcentagens
Na discussão a seguir, aprenderemos sobre algumas aplicações de porcentagens relacionadas a exemplos da vida real.
1. Descontos em compras: Imagine que você visita uma loja que oferece um desconto de 30% em um item de US$ 100. Você deve determinar 30% de $ 100 para calcular o valor que você economiza. Usando o cálculo:
30/100 = 0,3
0,3 × 100 = 30
Portanto, você economizará US$ 30 no item de US$ 100; você deve pagar apenas $ 70.
2. Pontuações dos exames: Em uma escola, um aluno tira 30 de 100 em um teste de matemática. Para determinar a pontuação percentual daquele aluno, precisamos calcular qual proporção representa 30 em 100. Usando a fórmula:
30/100 = 0,3
0,3 × 100 = 30%
Portanto, o aluno acertou 30% na prova de matemática.
3. Desempenho do mercado de ações: Suponha que você invista $ 100 em uma ação e ela aumente 30%. Para calcular o novo valor do seu investimento, você precisa encontrar 30% de US$ 100. Usando o método explicado acima:
normalização no banco de dados
30/100 = 0,3
0,3 × 100 = $ 30
O valor das ações aumentou em US$ 30, fazendo com que seu investimento valesse US$ 130.
4. Probabilidade: As porcentagens são usadas em cálculos de probabilidade; se houver 35% de probabilidade de chuva hoje, isso significa que em cada 100 situações climáticas semelhantes, espera-se que chova em 35.
5. Análise Estatística: As porcentagens são amplamente utilizadas na análise estatística para interpretar dados; eles ajudam a comparar proporções, calcular taxas de crescimento e compreender distribuições.
Alguns exemplos resolvidos
P. Quanto é 30% de 10?
Solução:
Etapa 1. 30% * 10
Etapa 2. 30% * 10 = (30/100) * 10
Etapa 3. 30% * 10 = (30/100) * 10 = 300/100 = 3
P. Quanto é 30% de 50?
Solução:
Etapa 1. 30% * 50
Etapa 2. 30% * 50 = (30/100) * 50
Etapa 3. 30% * 50 = (30/100) * 50 = 1.500/100 = 15
P. Quanto é 75% de 30?
Solução:
Etapa 1. 75% * 30
Etapa 2. 75% * 30 = (75/100) * 30
Etapa 3. 75% * 30 = (75/100) * 30 = 2.250/100 = 22,5
pilha em ds
P. Quanto é 28% de 100?
Solução:
Etapa 1. 28% * 100
Etapa 2. 28% * 100 = (28/100) * 100
Etapa 3. 28% * 100 = (28/100) * 100 = 2.800/100 = 28
P. Quanto é 30% de 20?
Solução:
Etapa 1. 30% * 20
Etapa 2. 30% * 20 = (30/100) * 20
Etapa 3. 30% * 20 = (30/100) * 20 = 600/100 = 6
P. Quanto é 30% de 200?
Solução:
Etapa 1. 30% * 200
Etapa 2. 30% * 200 = (30/100) * 200
Etapa 3. 30% * 200 = (30/100) * 200 = 6.000/100 = 60
Conclusão
As percentagens são um conceito fundamental da matemática que nos permite expressar proporções e fazer comparações. No nosso caso de calcular 30% de 100, multiplicamos o valor total por 30% (0,3) para obter o resultado, ou seja, 30. Esse conhecimento é sólido em matemática e aplicável em vários cenários do mundo real, como vendas, gorjetas e investimentos financeiros. Ao compreender percentagens e proporções, podemos melhorar as nossas capacidades de resolução de problemas e tomar decisões informadas em vários aspectos da vida.
