- O algoritmo de escalada é um algoritmo de busca local que se move continuamente na direção de aumentar a elevação/valor para encontrar o pico da montanha ou a melhor solução para o problema. Termina quando atinge um valor de pico onde nenhum vizinho tem um valor superior.
- O algoritmo de escalada é uma técnica usada para otimizar problemas matemáticos. Um dos exemplos amplamente discutidos de algoritmo de escalada é o problema do caixeiro viajante, no qual precisamos minimizar a distância percorrida pelo vendedor.
- Também é chamada de busca local gananciosa, pois olha apenas para o estado vizinho imediato e não além disso.
- Um nó do algoritmo de escalada possui dois componentes que são estado e valor.
- Hill Climbing é usado principalmente quando uma boa heurística está disponível.
- Neste algoritmo, não precisamos manter e manipular a árvore ou gráfico de pesquisa, pois ele mantém apenas um único estado atual.
Características da escalada:
A seguir estão alguns recursos principais do algoritmo de escalada:
Diagrama de espaço de estados para escalada:
A paisagem do espaço de estados é uma representação gráfica do algoritmo de escalada que mostra um gráfico entre vários estados do algoritmo e função objetivo/custo.
No eixo Y, pegamos a função que pode ser uma função objetivo ou função de custo, e o espaço de estados no eixo x. Se a função no eixo Y for custo, o objetivo da pesquisa é encontrar o mínimo global e o mínimo local. Se a função do eixo Y for uma função objetiva, então o objetivo da pesquisa é encontrar o máximo global e o máximo local.
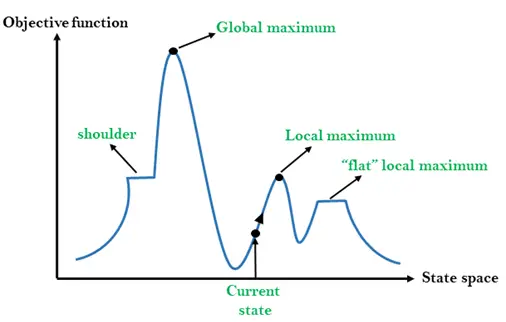
Diferentes regiões no cenário do espaço de estado:
Máximo Local: O máximo local é um estado melhor que os estados vizinhos, mas também existe outro estado que é superior a ele.
Máximo global: O máximo global é o melhor estado possível da paisagem do espaço de estados. Possui o maior valor da função objetivo.
Estado atual: É um estado em um diagrama de paisagem onde um agente está presente no momento.
Máximo local plano: É um espaço plano na paisagem onde todos os estados vizinhos dos estados atuais têm o mesmo valor.
Ombro: É uma região de planalto com uma borda ascendente.
mesa de látex
Tipos de algoritmo de escalada:
- Escalada simples:
- Subida mais íngreme:
- Escalada estocástica:
1. Escalada Simples:
A escalada simples é a maneira mais simples de implementar um algoritmo de escalada. Ele avalia apenas o estado do nó vizinho por vez e seleciona o primeiro que otimiza o custo atual e o define como estado atual . Ele apenas verifica se é um estado sucessor e, se for melhor que o estado atual, move-se para outro estado. Este algoritmo possui os seguintes recursos:
- Menos demorado
- Solução menos ideal e a solução não é garantida
Algoritmo para escalada simples:
- Se for um estado de meta, retorne o sucesso e desista.
- Caso contrário, se for melhor que o estado atual, atribua o novo estado como estado atual.
- Caso contrário, se não for melhor que o estado atual, retorne à etapa 2.
2. Subida mais íngreme:
O algoritmo de subida mais íngreme é uma variação do algoritmo simples de subida de colina. Este algoritmo examina todos os nós vizinhos do estado atual e seleciona um nó vizinho que está mais próximo do estado objetivo. Este algoritmo consome mais tempo enquanto procura vários vizinhos
Algoritmo para escalada em subida mais íngreme:
- Deixe SUCC ser um estado tal que qualquer sucessor do estado atual será melhor que ele.
- Para cada operador que se aplica ao estado atual:
- Aplique o novo operador e gere um novo estado.
- Avalie o novo estado.
- Se for um estado de meta, devolva-o e saia; caso contrário, compare-o com o SUCC.
- Se for melhor que SUCC, defina o novo estado como SUCC.
- Se o SUCC for melhor que o estado atual, defina o estado atual como SUCC.
3. Escalada estocástica:
A escalada estocástica não examina todos os seus vizinhos antes de se mover. Em vez disso, este algoritmo de busca seleciona um nó vizinho aleatoriamente e decide se o escolhe como estado atual ou examina outro estado.
Problemas no algoritmo de escalada:
1. Máximo Local: Um máximo local é um estado de pico na paisagem que é melhor do que cada um dos estados vizinhos, mas há outro estado também presente que é superior ao máximo local.
Solução: A técnica de retrocesso pode ser uma solução do máximo local na paisagem do espaço de estados. Crie uma lista do caminho promissor para que o algoritmo possa retroceder no espaço de busca e explorar outros caminhos também.

2. Planalto: Um platô é a área plana do espaço de busca na qual todos os estados vizinhos do estado atual contêm o mesmo valor, pois esse algoritmo não encontra a melhor direção para se mover. Uma busca em subidas pode se perder na área do planalto.
Solução: A solução para o platô é dar passos grandes ou muito pequenos durante a busca, para resolver o problema. Selecione aleatoriamente um estado que esteja longe do estado atual para que seja possível que o algoritmo encontre uma região não-platô.

3. Cumes: Uma crista é uma forma especial de máximo local. Tem uma área mais elevada do que as áreas circundantes, mas ela própria tem um declive e não pode ser alcançada com um único movimento.
Solução: Com o uso da busca bidirecional, ou movendo-se em diferentes direções, podemos melhorar esse problema.

Recozimento simulado:
Um algoritmo de escalada que nunca se move em direção a um valor inferior é garantido como incompleto porque pode ficar preso em um máximo local. E se o algoritmo aplicar um passeio aleatório, movendo um sucessor, então ele pode ser concluído, mas não eficiente. Recozimento simulado é um algoritmo que produz eficiência e integridade.
Em termos mecânicos anelamento é um processo de endurecimento de um metal ou vidro a uma alta temperatura e depois resfriar gradualmente, permitindo que o metal atinja um estado cristalino de baixa energia. O mesmo processo é usado no recozimento simulado, no qual o algoritmo escolhe um movimento aleatório, em vez de escolher o melhor movimento. Se o movimento aleatório melhorar o estado, ele seguirá o mesmo caminho. Caso contrário, o algoritmo segue o caminho que tem probabilidade menor que 1 ou desce e escolhe outro caminho.
