Neste artigo, discutiremos a travessia em árvore na estrutura de dados. O termo 'travessia de árvore' significa percorrer ou visitar cada nó de uma árvore. Existe uma única maneira de percorrer a estrutura de dados linear, como lista vinculada, fila e pilha. Considerando que existem várias maneiras de atravessar uma árvore listadas a seguir -
- Passagem de pré-encomenda
- Travessia em ordem
- Travessia de vale postal
Portanto, neste artigo, discutiremos as técnicas listadas acima para atravessar uma árvore. Agora, vamos começar a discutir as formas de atravessar as árvores.
Passagem de pré-encomenda
Esta técnica segue a política 'raiz esquerda direita'. Isso significa que, o primeiro nó raiz é visitado depois que a subárvore esquerda é percorrida recursivamente e, finalmente, a subárvore direita é percorrida recursivamente. Como o nó raiz é percorrido antes (ou pré) das subárvores esquerda e direita, isso é chamado de travessia de pré-ordem.
Portanto, em uma travessia de pré-ordem, cada nó é visitado antes de ambas as suas subárvores.
As aplicações de passagem de pré-pedido incluem -
- É usado para criar uma cópia da árvore.
- Também pode ser usado para obter a expressão de prefixo de uma árvore de expressão.
Algoritmo
Until all nodes of the tree are not visited Step 1 - Visit the root node Step 2 - Traverse the left subtree recursively. Step 3 - Traverse the right subtree recursively.
Exemplo
Agora, vamos ver o exemplo da técnica de travessia de pré-encomenda.
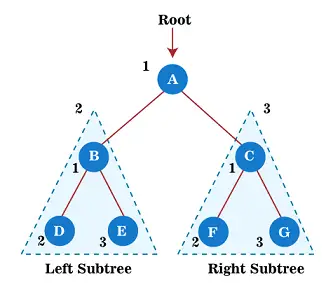
Agora, comece a aplicar o percurso de pré-ordem na árvore acima. Primeiro, percorremos o nó raiz A; depois disso, vá para sua subárvore esquerda B , que também será percorrido na pré-ordem.
Então, para a subárvore esquerda B, primeiro, o nó raiz B é atravessado por si mesmo; depois disso, sua subárvore esquerda D é percorrido. Desde o nó D não tem filhos, vá para a subárvore direita E . Como o nó E também não possui filhos, o percurso da subárvore esquerda do nó raiz A é concluído.
np.único
Agora, vá em direção à subárvore direita do nó raiz A que é C. Então, para a subárvore direita C, primeiro o nó raiz C atravessou-se; depois disso, sua subárvore esquerda F é percorrido. Desde o nó F não tem filhos, vá para a subárvore direita G . Como o nó G também não possui filhos, o percurso da subárvore direita do nó raiz A é concluído.
Portanto, todos os nós da árvore são percorridos. Portanto, a saída da travessia de pré-ordem da árvore acima é -
A → B → D → E → C → F → G
Para saber mais sobre a travessia de pré-pedido na estrutura de dados, você pode seguir o link Passagem de pré-encomenda .
Travessia de vale postal
Esta técnica segue a política de 'raiz esquerda-direita'. Isso significa que a primeira subárvore esquerda do nó raiz é percorrida, depois percorre recursivamente a subárvore direita e, finalmente, o nó raiz é percorrido. Como o nó raiz é percorrido após (ou pós) as subárvores esquerda e direita, ele é chamado de travessia pós-ordem.
Portanto, em uma travessia pós-ordem, cada nó é visitado após ambas as suas subárvores.
como converter um número inteiro em uma string em java
As aplicações de travessia pós-ordem incluem -
- É usado para deletar a árvore.
- Também pode ser usado para obter a expressão pós-fixada de uma árvore de expressão.
Algoritmo
Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Traverse the right subtree recursively. Step 3 - Visit the root node.
Exemplo
Agora, vamos ver o exemplo da técnica de travessia pós-ordem.

Agora, comece a aplicar o percurso pós-ordem na árvore acima. Primeiro, percorremos a subárvore esquerda B que será percorrida em pós-ordem. Depois disso, percorreremos a subárvore certa C em pós-ordem. E finalmente, o nó raiz da árvore acima, ou seja, A , é percorrido.
tente pegar o bloco em java
Então, para a subárvore esquerda B, primeiro, sua subárvore esquerda D é percorrido. Desde o nó D não tem filhos, percorra a subárvore certa E . Como o nó E também não possui filhos, vá para o nó raiz B. Depois de atravessar o nó B, a travessia da subárvore esquerda do nó raiz A é concluída.
Agora, vá em direção à subárvore direita do nó raiz A que é C. Portanto, para a subárvore direita C, primeiro sua subárvore esquerda F é percorrido. Desde o nó F não tem filhos, percorra a subárvore certa G . Como o nó G também não possui filhos, portanto, finalmente, o nó raiz da subárvore direita, ou seja, C, é percorrido. A travessia da subárvore direita do nó raiz A é concluída.
Por fim, percorra o nó raiz de uma determinada árvore, ou seja, A . Depois de percorrer o nó raiz, o percurso pós-ordem da árvore fornecida é concluído.
Portanto, todos os nós da árvore são percorridos. Portanto, a saída da travessia pós-ordem da árvore acima é -
D → E → B → F → G → C → A
Para saber mais sobre o percurso pós-ordem na estrutura de dados, você pode seguir o link Travessia de vale postal .
Travessia em ordem
Esta técnica segue a política 'esquerda, raiz, direita'. Isso significa que a primeira subárvore esquerda é visitada após o nó raiz ser percorrido e, finalmente, a subárvore direita é percorrida. Como o nó raiz é percorrido entre as subárvores esquerda e direita, ele é denominado travessia em ordem.
Assim, na travessia em ordem, cada nó é visitado entre suas subárvores.
As aplicações de travessia Inorder incluem -
- É usado para obter os nós BST em ordem crescente.
- Também pode ser usado para obter a expressão de prefixo de uma árvore de expressão.
Algoritmo
Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Visit the root node. Step 3 - Traverse the right subtree recursively.
Exemplo
Agora, vamos ver o exemplo da técnica de travessia Inorder.

Agora, comece a aplicar o percurso inorder na árvore acima. Primeiro, percorremos a subárvore esquerda B que será percorrido em ordem. Depois disso, percorreremos o nó raiz A . E finalmente, a subárvore certa C é percorrido em ordem.
Então, para a subárvore esquerda B , primeiro, sua subárvore esquerda D é percorrido. Desde o nó D não tem filhos, então depois de percorrê-lo, o nó B será percorrido e, por fim, a subárvore direita do nó B, ou seja E , é percorrido. O nó E também não tem filhos; portanto, a travessia da subárvore esquerda do nó raiz A é concluída.
Depois disso, percorra o nó raiz de uma determinada árvore, ou seja, A .
Por fim, vá em direção à subárvore direita do nó raiz A que é C. Portanto, para a subárvore direita C; primeiro, sua subárvore esquerda F é percorrido. Desde o nó F não tem filhos, nó C será percorrido e, por fim, uma subárvore direita do nó C, ou seja, G , é percorrido. O nó G também não tem filhos; portanto, a travessia da subárvore direita do nó raiz A é concluída.
À medida que todos os nós da árvore são percorridos, a travessia em ordem da árvore fornecida é concluída. A saída da travessia em ordem da árvore acima é -
D → B → E → A → F → C → G
Para saber mais sobre o percurso inorder na estrutura de dados, você pode seguir o link Travessia Inorder .
java int para dobrar
Complexidade das técnicas de passagem em árvore
A complexidade de tempo das técnicas de passagem em árvore discutidas acima é Sobre) , onde 'e' é o tamanho da árvore binária.
Considerando que a complexidade espacial das técnicas de passagem de árvores discutidas acima é O(1) se não considerarmos o tamanho da pilha para chamadas de função. Caso contrário, a complexidade espacial destas técnicas é Oh) , onde 'h' é a altura da árvore.
Implementação de travessia em árvore
Agora, vamos ver a implementação das técnicas discutidas acima usando diferentes linguagens de programação.
Programa: Escreva um programa para implementar técnicas de travessia de árvores em C.
#include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; printf(' %d ', root->element); traversePreorder(root->left); traversePreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); printf(' %d ', root->element); traverseInorder(root->right); } /*function to traverse the nodes of binary tree in postorder*/ void traversePostorder(struct node* root) { if (root == NULL) return; traversePostorder(root->left); traversePostorder(root->right); printf(' %d ', root->element); } int main() { struct node* root = createNode(36); root->left = createNode(26); root->right = createNode(46); root->left->left = createNode(21); root->left->right = createNode(31); root->left->left->left = createNode(11); root->left->left->right = createNode(24); root->right->left = createNode(41); root->right->right = createNode(56); root->right->right->left = createNode(51); root->right->right->right = createNode(66); printf('
The Preorder traversal of given binary tree is -
'); traversePreorder(root); printf('
The Inorder traversal of given binary tree is -
'); traverseInorder(root); printf('
The Postorder traversal of given binary tree is -
'); traversePostorder(root); return 0; } Saída

Programa: Escreva um programa para implementar técnicas de passagem de árvore em C#.
using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traversePreorder(Node node) { if (node == null) return; Console.Write(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); Console.Write(node.value + ' '); traverseInorder(node.right); } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); Console.Write(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(37); bt.root.left = new Node(27); bt.root.right = new Node(47); bt.root.left.left = new Node(22); bt.root.left.right = new Node(32); bt.root.left.left.left = new Node(12); bt.root.left.left.right = new Node(25); bt.root.right.left = new Node(42); bt.root.right.right = new Node(57); bt.root.right.right.left = new Node(52); bt.root.right.right.right = new Node(67); Console.WriteLine('The Preorder traversal of given binary tree is - '); bt.traversePreorder(); Console.WriteLine(); Console.WriteLine('The Inorder traversal of given binary tree is - '); bt.traverseInorder(); Console.WriteLine(); Console.WriteLine('The Postorder traversal of given binary tree is - '); bt.traversePostorder(); } } Saída

Programa: Escreva um programa para implementar técnicas de passagem de árvore em C++.
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; cout<<' '<element<left); traversepreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); cout<<' '<element<right); } *function to traverse the nodes of binary tree in postorder* void traversepostorder(struct node* root) { if (root="=" null) return; traversepostorder(root->left); traversePostorder(root->right); cout<<' '<element<left="createNode(28);" root->right = createNode(48); root->left->left = createNode(23); root->left->right = createNode(33); root->left->left->left = createNode(13); root->left->left->right = createNode(26); root->right->left = createNode(43); root->right->right = createNode(58); root->right->right->left = createNode(53); root->right->right->right = createNode(68); cout<<'
the preorder traversal of given binary tree is -
'; traversepreorder(root); cout<<'
inorder traverseinorder(root); postorder traversepostorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-6.webp" alt="Tree Traversal"> <p> <strong>Program:</strong> Write a program to implement tree traversal techniques in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class Tree { Node root; /* root of the tree */ Tree() { root = null; } /*function to print the nodes of given binary in Preorder*/ void traversePreorder(Node node) { if (node == null) return; System.out.print(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } /*function to print the nodes of given binary in Inorder*/ void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } /*function to print the nodes of given binary in Postorder*/ void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); System.out.print(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } public static void main(String args[]) { Tree pt = new Tree(); pt.root = new Node(36); pt.root.left = new Node(26); pt.root.right = new Node(46); pt.root.left.left = new Node(21); pt.root.left.right = new Node(31); pt.root.left.left.left = new Node(11); pt.root.left.left.right = new Node(24); pt.root.right.left = new Node(41); pt.root.right.right = new Node(56); pt.root.right.right.left = new Node(51); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Preorder traversal of given binary tree is - '); pt.traversePreorder(); System.out.println('
'); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println('
'); System.out.println('The Postorder traversal of given binary tree is - '); pt.traversePostorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-7.webp" alt="Tree Traversal"> <h2>Conclusion</h2> <p>In this article, we have discussed the different types of tree traversal techniques: preorder traversal, inorder traversal, and postorder traversal. We have seen these techniques along with algorithm, example, complexity, and implementation in C, C++, C#, and java.</p> <p>So, that's all about the article. Hope it will be helpful and informative to you.</p> <hr></'
></'></'></'> Saída
multiplexação
Após a execução do código acima, a saída será -

Conclusão
Neste artigo, discutimos os diferentes tipos de técnicas de travessia de árvore: travessia de pré-ordem, travessia de ordem e travessia de pós-ordem. Vimos essas técnicas junto com algoritmo, exemplo, complexidade e implementação em C, C++, C# e java.
Então, isso é tudo sobre o artigo. Espero que seja útil e informativo para você.
