- Autômatos pushdown são uma maneira de implementar um CFG da mesma forma que projetamos um DFA para uma gramática regular. Um DFA pode lembrar uma quantidade finita de informações, mas um PDA pode lembrar uma quantidade infinita de informações.
- O autômato pushdown é simplesmente um NFA aumentado com uma 'memória de pilha externa'. A adição de pilha é usada para fornecer um recurso de gerenciamento de memória last-in-first-out para autômatos Pushdown. Os autômatos pushdown podem armazenar uma quantidade ilimitada de informações na pilha. Ele pode acessar uma quantidade limitada de informações na pilha. Um PDA pode colocar um elemento no topo da pilha e retirar um elemento do topo da pilha. Para ler um elemento na pilha, os elementos superiores devem ser retirados e perdidos.
- Um PDA é mais poderoso que FA. Qualquer linguagem que possa ser aceita pela FA também pode ser aceita pelo PDA. O PDA também aceita uma classe de linguagem que nem mesmo pode ser aceita pela FA. Assim, o PDA é muito mais superior ao FA.
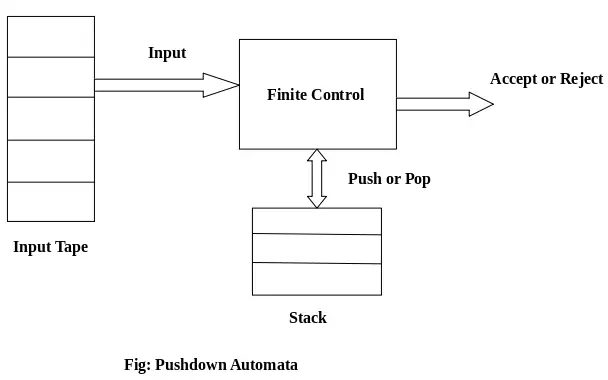
Componentes do PDA:
Fita de entrada: A fita de entrada é dividida em muitas células ou símbolos. O cabeçote de entrada é somente leitura e só pode se mover da esquerda para a direita, um símbolo por vez.
Controle finito: O controle finito possui algum ponteiro que aponta o símbolo atual que deve ser lido.
Pilha: A pilha é uma estrutura na qual podemos empurrar e remover os itens apenas de uma extremidade. Tem um tamanho infinito. No PDA, a pilha é usada para armazenar os itens temporariamente.
Definição formal de PDA:
O PDA pode ser definido como uma coleção de 7 componentes:
P: o conjunto finito de estados
∑: o conjunto de entrada
C: um símbolo de pilha que pode ser empurrado e retirado da pilha
q0: o estado inicial
como transformar string em int
COM: um símbolo inicial que está em Γ.
F: um conjunto de estados finais
d: função de mapeamento que é usada para passar do estado atual para o próximo estado.
Descrição Instantânea (ID)
ID é uma notação informal de como um PDA calcula uma string de entrada e toma uma decisão de que a string seja aceita ou rejeitada.
Uma descrição instantânea é uma tripla (q, w, α) onde:
q descreve o estado atual.
Em descreve a entrada restante.
exemplo de substring java
a descreve o conteúdo da pilha, no canto superior esquerdo.
Notação de catraca:
O sinal ⊢ descreve a notação da catraca e representa um movimento.
O sinal ⊢* descreve uma sequência de movimentos.
Por exemplo,
(p, b, T) ⊢ (q, w, α)
No exemplo acima, ao fazer uma transição do estado p para q, o símbolo de entrada 'b' é consumido e o topo da pilha 'T' é representado por uma nova string α.
Exemplo 1:
Projete um PDA para aceitar um idiomanb2n.
Solução: Nesta linguagem, n número de a's deve ser seguido por 2n número de b's. Portanto, aplicaremos uma lógica muito simples: se lermos um único 'a', colocaremos dois as na pilha. Assim que lermos 'b', para cada 'b', apenas um 'a' deverá ser retirado da pilha.
java classificando uma lista
O ID pode ser construído da seguinte forma:
δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa)
Agora, quando lermos b, mudaremos o estado de q0 para q1 e começaremos a exibir o 'a' correspondente. Por isso,
δ(q0, b, a) = (q1, ε)
Assim, este processo de estourar 'b' será repetido a menos que todos os símbolos sejam lidos. Observe que a ação de popping ocorre apenas no estado q1.
δ(q1, b, a) = (q1, ε)
Depois de ler todos os b's, todos os a's correspondentes devem ser exibidos. Portanto, quando lemos ε como símbolo de entrada, não deve haver nada na pilha. Portanto o movimento será:
δ(q1, ε, Z) = (q2, ε)
Onde
qual é o tamanho da tela do meu monitor
PDA = ({q0, q1, q2}, {a, b}, {a, Z}, δ, q0, Z, {q2})
Podemos resumir o ID como:
δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa) δ(q0, b, a) = (q1, ε) δ(q1, b, a) = (q1, ε) δ(q1, ε, Z) = (q2, ε)
Agora simularemos este PDA para a string de entrada 'aaabbbbbbb'.
δ(q0, aaabbbbbb, Z) ⊢ δ(q0, aabbbbbb, aaZ) ⊢ δ(q0, abbbbbb, aaaaZ) ⊢ δ(q0, bbbbbb, aaaaaaZ) ⊢ δ(q1, bbbbb, aaaaaZ) ⊢ δ(q1, bbbb, aaaaZ) ⊢ δ(q1, bbb, aaaZ) ⊢ δ(q1, bb, aaZ) ⊢ δ(q1, b, aZ) ⊢ δ(q1, ε, Z) ⊢ δ(q2, ε) ACCEPT
Exemplo 2:
Projete um PDA para aceitar um idioma 0n1eu0n.
Solução: Neste PDA, n número de 0's são seguidos por qualquer número de 1's seguido n número de 0's. Portanto, a lógica para o projeto de tal PDA será a seguinte:
Coloque todos os 0 na pilha ao encontrar os primeiros 0. Então, se lermos 1, simplesmente não faça nada. Em seguida, leia 0 e, em cada leitura de 0, retire um 0 da pilha.
Por exemplo:

Este cenário pode ser escrito no formulário de ID como:
δ(q0, 0, Z) = δ(q0, 0Z) δ(q0, 0, 0) = δ(q0, 00) δ(q0, 1, 0) = δ(q1, 0) δ(q0, 1, 0) = δ(q1, 0) δ(q1, 0, 0) = δ(q1, ε) δ(q0, ε, Z) = δ(q2, Z) (ACCEPT state)
Agora simularemos este PDA para a string de entrada '0011100'.
δ(q0, 0011100, Z) ⊢ δ(q0, 011100, 0Z) ⊢ δ(q0, 11100, 00Z) ⊢ δ(q0, 1100, 00Z) ⊢ δ(q1, 100, 00Z) ⊢ δ(q1, 00, 00Z) ⊢ δ(q1, 0, 0Z) ⊢ δ(q1, ε, Z) ⊢ δ(q2, Z) ACCEPT
