Dada uma string, encontre todas as maneiras de quebrar a string fornecida em forma de suporte. Inclua cada substring dentro de um parêntese.
comandos sqlddl
Exemplos:
Input : abc Output: (a)(b)(c) (a)(bc) (ab)(c) (abc) Input : abcd Output : (a)(b)(c)(d) (a)(b)(cd) (a)(bc)(d) (a)(bcd) (ab)(c)(d) (ab)(cd) (abc)(d) (abcd)
Recomendamos fortemente que você minimize seu navegador e tente isso mesmo primeiro.
A idéia é usar a recursão. Mantemos dois parâmetros - índice do próximo caractere a ser processado e a sequência de saída até agora. Começamos do índice do próximo caractere a ser processado, anexando a substring formada pela string não processada à sequência de saída e recorrente à string restante até processarmos a sequência inteira. Usamos o STD :: Substr para formar a sequência de saída. Substr (Pos N) Retorna uma substring de comprimento n que começa na posição POS da string atual.
Abaixo do diagrama mostra a árvore de recursão para a sequência de entrada 'ABC'. Cada nó no diagrama mostra string processada (marcada por verde) e string não processada (marcada por vermelho).
sabe
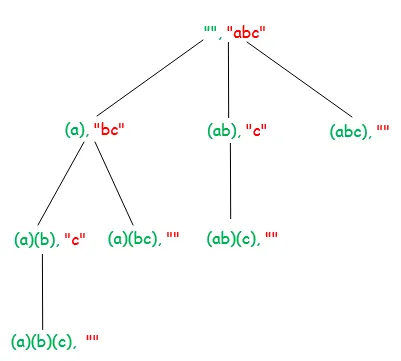
Abaixo está a implementação da ideia acima
C++// C++ Program to find all combinations of Non- // overlapping substrings formed from given // string #include
// Java program to find all combinations of Non- // overlapping substrings formed from given // string class GFG { // find all combinations of non-overlapping // substrings formed by input string str static void findCombinations(String str int index String out) { if (index == str.length()) System.out.println(out); for (int i = index; i < str.length(); i++) // append substring formed by str[index // i] to output string findCombinations(str i + 1 out + '(' + str.substring(index i+1) + ')' ); } // Driver Code public static void main (String[] args) { // input string String str = 'abcd'; findCombinations(str 0 ''); } } // Contributed by Pramod Kumar
# Python3 Program to find all combinations of Non- # overlapping substrings formed from given # string # find all combinations of non-overlapping # substrings formed by input string str # index – index of the next character to # be processed # out - output string so far def findCombinations(string index out): if index == len(string): print(out) for i in range(index len(string) 1): # append substring formed by str[index # i] to output string findCombinations(string i + 1 out + '(' + string[index:i + 1] + ')') # Driver Code if __name__ == '__main__': # input string string = 'abcd' findCombinations(string 0 '') # This code is contributed by # sanjeev2552
// C# program to find all combinations // of Non-overlapping substrings formed // from given string using System; class GFG { // find all combinations of non-overlapping // substrings formed by input string str public static void findCombinations(string str int index string @out) { if (index == str.Length) { Console.WriteLine(@out); } for (int i = index; i < str.Length; i++) { // append substring formed by // str[index i] to output string findCombinations( str i + 1 @out + '(' + str.Substring(index (i + 1) - index) + ')'); } } // Driver Code public static void Main(string[] args) { // input string string str = 'abcd'; findCombinations(str 0 ''); } } // This code is contributed by Shrikant13
// Javascript program for the above approach // find all combinations of non-overlapping // substrings formed by input string str // index – index of the next character to // be processed // out - output string so far function findCombinations(string index out) { if (index == string.length) { console.log(out); } for (let i = index; i < string.length; i++) { // append substring formed by str[index // i] to output string findCombinations(string i + 1 out + '(' + string.substring(index i + 1) + ')'); } } // Driver Code const string = 'abcd'; findCombinations(string 0 ''); // contributed by adityasharmadev01
Saída
(a)(b)(c)(d) (a)(b)(cd) (a)(bc)(d) (a)(bcd) (ab)(c)(d) (ab)(cd) (abc)(d) (abcd)
Complexidade do tempo: o (n2)
Espaço auxiliar: o (n2)
componentes do robô
